
【题目】已知线段AB=60cm.
![]()
(1)如图1,点P沿线段AB自A点向B点以2厘米/秒运动,同时点Q沿线段BA自B点 向A点以4厘米/秒运动,问经过几秒后P、Q相遇?
(2)在(1)的条件下,几秒钟后,P、Q相距12cm?
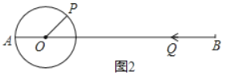
(3)如图2,AO=PO=10厘米,∠POB=40°,点P绕着点O以10度/秒的速度顺时针 旋转一周停止,同时点Q沿线段BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度.
【答案】(1) 经过10秒钟后P、Q相遇;(2) 经过8秒钟或12秒钟后,P、Q相距12cm;(3) 点Q运动的速度为10cm/s或![]() cm/s.
cm/s.
【解析】
(1)根据相遇问题中的等量关系列方程求解即可;
(2)分相遇前相距12cm和相遇后相距12cm,分别列方程求解即可;
(3)由于点P,Q只能在直线AB上相遇,所以可先求出点P两次旋转到直线AB上的时间,然后分别列出方程求解即可.
解:(1)设经过t秒后P、Q相遇,
由题意得:2t+4t=60,
解得t=10,
答:经过10秒钟后P、Q相遇;
(2)设经过x秒P、Q相距12cm,
当相遇前相距12cm时,
由题意得:2x+4x+12=60,
解得:x=8,
当相遇后相距12cm时,
由题意得:2x+4x-12=60,
解得:x=12,
答:经过8秒钟或12秒钟后,P、Q相距12cm;
(3)设点Q运动的速度为ycm/s,
∵点P,Q只能在直线AB上相遇,
∴点P第一次旋转到直线AB上的时间为:40÷10=4s,
若此时相遇,则4y=60-20,
解得:y=10,
点P第二次旋转到直线AB上的时间为:(40+180)÷10=22s,
若此时相遇,则22y=60,
解得:y=![]() ,
,
答:点Q运动的速度为10cm/s或![]() cm/s.
cm/s.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】[ 问题提出 ]
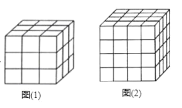
一个边长为 ncm(n3)的正方体木块,在它的表面涂上颜色,然后切成边长为1cm的小正方体木块,没有涂上颜色的有多少块?只有一面涂上颜色的有多少块?有两面涂上颜色的有多少块?有三面涂上颜色的多少块?
[ 问题探究 ]
我们先从特殊的情况入手
(1)当n=3时,如图(1)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有1×1×1=1个小正方体;
一面涂色的:在面上,每个面上有1个,共有6个;
两面涂色的:在棱上,每个棱上有1个,共有12个;
三面涂色的:在顶点处,每个顶点处有1个,共有8个.
(2)当n=4时,如图(2)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有2×2×2=8个小正方体:
一面涂色的:在面上,每个面上有4个,正方体共有 个面,因此一面涂色的共有 个;
两面涂色的:在棱上,每个棱上有2个,正方体共有 条棱,因此两面涂色的共有 个;
三面涂色的:在顶点处,每个顶点处有1个,正方体共有 个顶点,因此三面涂色的共有 个…
[ 问题解决 ]
一个边长为ncm(n3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有______个小正方体;一面涂色的:在面上,共有______个; 两面涂色的:在棱上,共有______个; 三面涂色的:在顶点处,共______个。
[ 问题应用 ]
一个大的正方体,在它的表面涂上颜色,然后把它切成棱长1cm的小正方体,发现有两面涂色的小正方体有96个,请你求出这个大正方体的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公园门票价格规定如下表:
购票张数 | 1~50张 | 51~100张 | 100张以上 |
每张票的价格 | 15元 | 13元 | 11元 |
某校七年级(1)(2)两个班共102人去游园,其中(1)班超过40人,不足50人,经估算,如果两个班都以班为单位购票,则一共应付1422元.问:
(1)两个班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可比两个班都以班为单位购票省多少元钱?
(2)如果七年级(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
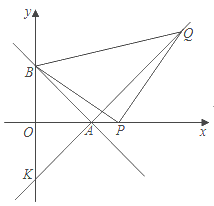
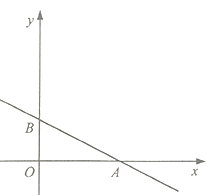
【题目】如图,直线AB:y=﹣x﹣b分别与x、y轴交于A(6,0)、B两点.
(1)求直线AB的解析式;
(2)若P为A点右侧x轴上的一动点,以P为直角顶点,BP为腰在第一象限内作等腰直角△BPQ,连接QA并延长交y轴于点K,当P点运动时,K点的位置是否发生变化?若不变,请求出它的坐标;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,已知∠BAD=120°,∠EGF=60°, ∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC、CD于E、F.
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/6b570bc424f747a8be031e9f971720ec.png]
(1)如图甲,当顶点G运动到与点A重合时,求证:EC+CF=BC;
(2)知识探究:
①如图乙,当顶点G运动到AC的中点时,请直接写出线段EC、CF与BC的数量关系(不需要写出证明过程);
②如图丙,在顶点G运动的过程中,若![]() ,探究线段EC、CF与BC的数量关系;
,探究线段EC、CF与BC的数量关系;
(3)问题解决:如图丙,已知菱形的边长为8,BG=7,CF=![]() ,当
,当![]() >2时,求EC的长度。
>2时,求EC的长度。
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/1671b8ec524a49feac7097357d4ff9a8.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() (
(![]() )交
)交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(2)若点![]() 是直线
是直线![]() 上的任意一点,且点
上的任意一点,且点![]() 与点
与点![]() 距离的最小值为4,求该直线表达式;
距离的最小值为4,求该直线表达式;
(3)在(2)的基础上,若点![]() 在第一象限,且
在第一象限,且![]() 为等腰直角三角形,求点
为等腰直角三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,它表示甲乙两人从同一个地点出发后的情况。到10:00时,甲大约走了13千米。根据图象回答:
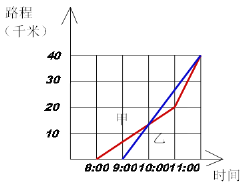
(1)甲是几点钟出发?
(2)乙是几点钟出发,到十点时,他大约走了多少千米?
(3)到10:00为止,哪个人的速度快?
(4)两人在途中有几次相遇?分别在几点钟相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数),并且运算重复进行,例如,取n=26,第三次“F运算”的结果是11.若n=111,则第2019次“F运算”的结果是_____.
为奇数的正整数),并且运算重复进行,例如,取n=26,第三次“F运算”的结果是11.若n=111,则第2019次“F运算”的结果是_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
![]()
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com