
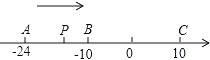
����Ŀ����֪��������A��B��C�����㣬�ֱ��ʾ��������24����10��10������P��A��������ÿ��1����λ���ٶ����յ�C�ƶ������ƶ�ʱ��Ϊt�룮
��1���ú�t�Ĵ���ʽ��ʾP����A�͵�C�ľ��룺
PA=________��PC=________��
��2������P�˶���B��ʱ����Q��A���������ÿ��3����λ���ٶ���C���˶���Q�㵽��C�����������ͬ�����ٶȷ��أ��˶����յ�A���ڵ�Q��ʼ�˶���P��Q����֮��ľ����ܷ�Ϊ2����λ������ܣ��������ʱ��P��ʾ������������ܣ���˵�����ɣ�
���𰸡���1��t��34��t����2����P��ʾ����Ϊ��4����2��3��4 .
��������
������1������P��λ�ý����ó�PA��PC�ľ��룻
��2���ֱ����P����Q������ǰ�Լ�������������ۣ������ֱ�����ó����ɣ�
�����������1���߶���P��A��������ÿ��1����λ���ٶ����յ�C�ƶ������ƶ�ʱ��Ϊt�룬
��P����A�ľ���Ϊ��PA=t��P����C�ľ���Ϊ��PC=��24+10��-t=34-t��
�ʴ�Ϊ��t��34-t��
��2����P����Q���Ҳ࣬��Q�㻹û����P��ʱ��
3t+2=14+t��
��ã�t=6��
����ʱ��P��ʾ����Ϊ��4��
��P����Q����࣬��Q����P������2����λ��
3t��2=14+t��ã�t=8��
����ʱ��P��ʾ����Ϊ��2��
��Q�㵽��C���P����Q�����ʱ��
14+t+2+3t��34=34
��ã�t=13��
����ʱ��P��ʾ����Ϊ3��
��Q�㵽��C���P����Q���Ҳ�ʱ��
14+t��2+3t��34=34
��ã�t=14��
����ʱ��P��ʾ����Ϊ4��
������������P��ʾ����Ϊ��4����2��3��4 .


 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�����װ�н���ɫ��ͬ��20��С�����к���6��������14��
��1���ȴӴ�����ȡ��x��x��3����������ٴӴ������������1����������������Ϊ�¼�A����������б���
�¼�A | ��Ȼ�¼� | ����¼� |
x��ֵ |
��2���ȴӴ�����ȡ��m�������ٷ���2m��һ���ĺ���ҡ�ȣ��������1�����Ǻ���ĸ�����![]() ����m��ֵ��
����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90����DΪCB��һ�㣬����D��DE��AB�ڵ�E��
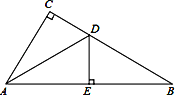
(1)��CD=DE���жϡ�CAD���BAD��������ϵ��
(2)��AE=EB��CB=10��AC=5,���ACD���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
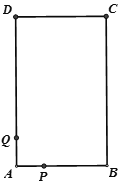
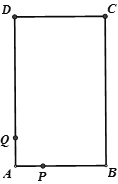
����Ŀ����ͼ��������ABCD�У�AB=4cm��BC=6cm������һ����P��A������2cm/����ٶȣ��ؾ��εı�A��B��C��D�ص���A�����P���˶�ʱ��Ϊt�룬
(1)��t=3��ʱ����BP�ij���
(2)��tΪ��ֵʱ������BP��AP����ABP�����Ϊ�����ε��������֮һ��
(3)QΪAD���ϵĵ㣬��DQ=5����tΪ��ֵʱ���Գ����ε��������㼰��PΪ��������������DCQȫ�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ���һ���������ܱ�ʾΪ��������������ƽ�����ô���dz����������Ϊ����г��������8=32-12��16=52-32��24=72-52����ˣ�8��16��24����������������г������
��1����32��75��80���������У��Ǻ�г������______��
��2����200Ϊ��г������200����д����������������ƽ��������������������ĺ�Ϊ______��
��3��С��ͨ���۲췢���������������г������Ϊ8�ı�������������������Ϊ2n-1��2n+1������nȡ��������������ͨ��������֤����г����8�ı�������������Ƿ���ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ��������У���ƻ������ס������ֹ����������¹�����ͼ�飬���鷢�֣�������������3�����������2���������ʽ�1020Ԫ��������������4�����������3���������ʽ�1440Ԫ��
��1���ס����������ÿ���ļ۸�ֱ��Ƕ���Ԫ��
��2������У�ƻ����������ֹ������20�������������������������ڼ�������������ѧУ�����ܹ��ṩ�ʽ�4320Ԫ������Ƽ��ֹ��������ѧУѡ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A=2a2+3ab��2a��1��B=��a2+![]() ab+
ab+![]() ��
��
��1��a=��1��b=��2ʱ����4A����3A��2B����ֵ��
��2������1����ʽ�ӵ�ֵ��a��ȡֵ�أ���b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��B��C�ֱ��ǡ�PAQ������AP��AQ�ϵĵ㣬ֱ��l��ֱƽ��BC��

��1���߹���ͼ����ֱ��1������һ��O��ʹ�õ�O��AP��AQ�������(��д������������ͼ�ۼ�)��
��2����O����OE��AP��OF��AQ������ֱ�ΪE��F����֤BE=CF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AC=BC����ACB=90������D��E��AB�ϣ�����ACD����BCE�ֱ���CD��CE���ۣ���A��B�ֱ����ڵ�A����B����λ�ã��ٽ���A��CD����B��CE�ֱ���A��C��B��C���ۣ���D���Eǡ���غ��ڵ�O�����A��OB���Ķ�����_________��
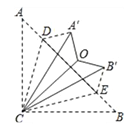
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com