
����Ŀ�� ���һ���������ܱ�ʾΪ��������������ƽ�����ô���dz����������Ϊ����г��������8=32-12��16=52-32��24=72-52����ˣ�8��16��24����������������г������
��1����32��75��80���������У��Ǻ�г������______��
��2����200Ϊ��г������200����д����������������ƽ��������������������ĺ�Ϊ______��
��3��С��ͨ���۲췢���������������г������Ϊ8�ı�������������������Ϊ2n-1��2n+1������nȡ��������������ͨ��������֤����г����8�ı�������������Ƿ���ȷ��
���𰸡���1��32��80����2��100����3������г����8�ı����������������ȷ�ģ�֤���������
��������
��1�����ݡ���г�����Ķ��壬���һ������������г��Ӧ����ʲô�������Դ������ж�32��75��80���������У���Щ���Ǻ�г����
��2������ĸ��ʾ���������������г�����ɺ�г����200���г����̣�������õ��������������������Ӷ�����������������������ĺͣ�
��3������ĸ��ʾ���������������г����ͨ��������֤�����۳�����
�⣺��1���ɡ���г�����Ķ��壬�������������������ֱ�Ϊ![]() ��
��![]() ��
��
���г���ɱ�ʾΪ��![]() ��������
��������![]() ��ʾ��������
��ʾ��������
�ࡰ��г��������8������������
��32��80����г����75���Ǻ�г������32=92-72��80=212-192��
�ʴ�Ϊ��32��80.
��2����![]() 200����
200����![]() 200��
200��
��![]() ��
��
��![]() ��
��![]() ��
��
��49+51=100��
�����������������ĺ�Ϊ100��
�ʴ�Ϊ��100.
��3��֤������![]() ,
,
�ࡰ��г����8�ı����������������ȷ�ģ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ��1������֪������ABC�У���BAC��90����AB=AC��ֱ��m������A��BD��ֱ��m, CE��ֱ��m,����ֱ�Ϊ��D��E.֤��:DE=BD+CE.
��2�� ��ͼ��2��������1���е�������Ϊ������ABC�У�AB=AC��D��A��E���㶼��ֱ��m��,��������BDA=��AEC=��BAC=![]() ,����
,����![]() Ϊ������ǻ�۽�.���ʽ���DE=BD+CE�Ƿ����?�����,�������֤��;��������,��˵������.
Ϊ������ǻ�۽�.���ʽ���DE=BD+CE�Ƿ����?�����,�������֤��;��������,��˵������.
��3����չ��Ӧ�ã���ͼ��3����D��E��D��A��E��������ֱ��m�ϵ������㣨D��A��E���㻥���غϣ�,��FΪ��BACƽ�����ϵ�һ��,����ABF����ACF��Ϊ�ȱ������Σ�����BD��CE,����BDA=��AEC=��BAC�����ж���DEF����״.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������߶�AB��2(��λ����)���߶�CD��4(��λ����)����A�������ϱ�ʾ�����ǣ�10����C�������ϱ�ʾ������16.���߶�AB��ÿ��6����λ���ȵ��ٶ����������˶���ͬʱ�߶�CD��ÿ��2����λ���ȵ��ٶ����������˶������˶�ʱ��Ϊt s.
(1)����B���C����ʱ����A����D�������ϱ�ʾ�����ֱ�Ϊ________��
(2)��tΪ��ֵʱ����B�պ����߶�CD���е��غϣ�
(3)���˶���BC��8(��λ����)ʱ�������ʱ��B�������ϱ�ʾ������
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ij����ѧ�����У�����Ϊ100�֣����������ݼ���ռ��ֵ�ķֲ������������ͳ��ͼ�������½�����ȷ���ǣ�������
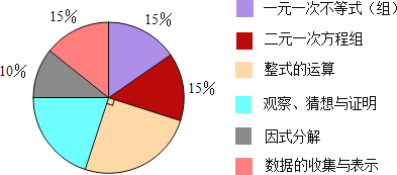
��һԪһ�β���ʽ���飩�������Ԫһ�η����鲿����ռ��ֵһ��
����ʽ�ֽⲿ�����Ծ���ռ10��
����ʽ�����㲿���������Ծ�����ռ����Ϊ25%
�ܹ۲졢������֤�����ֵ�Բ�ĽǶ���Ϊ72��
A.�٢ڢ�B.�ڢۢ�C.�٢�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����ֱ�������Ӧ�ļ����ڣ�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��ÿ����
��ÿ���� ![]() ֮����������
֮���������� ![]() ��
�� ![]() ����
����
��1���������ϣ�{ ��}��
��2���������ϣ�{ ��}��
��3���������ϣ�{ ��}��
��4�����������ϣ�{ ��}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
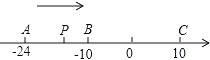
����Ŀ����֪��������A��B��C�����㣬�ֱ��ʾ��������24����10��10������P��A��������ÿ��1����λ���ٶ����յ�C�ƶ������ƶ�ʱ��Ϊt�룮
��1���ú�t�Ĵ���ʽ��ʾP����A�͵�C�ľ��룺
PA=________��PC=________��
��2������P�˶���B��ʱ����Q��A���������ÿ��3����λ���ٶ���C���˶���Q�㵽��C�����������ͬ�����ٶȷ��أ��˶����յ�A���ڵ�Q��ʼ�˶���P��Q����֮��ľ����ܷ�Ϊ2����λ������ܣ��������ʱ��P��ʾ������������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��,���ı���ABCD�ı�AB����ȡһ��E(��E����A,B�غ�),�ֱ�����ED,EC,�����ı���ABCD�ֳ�����������,�����������������������,���ǾͰ�E�����ı���ABCD�ı�AB�ϵġ����Ƶ㡱;��������������ζ�����,���ǾͰ�E�����ı���ABCD�ı�AB�ϵġ�ǿ���Ƶ㡱.
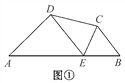
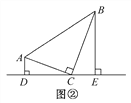
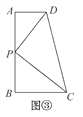
���������֡���ͼ��,�ڡ�ABC��,��ACB=90��,ֱ�Ƕ���C��ֱ��DE��,�ֱ����A,B��AD��DE�ڵ�D,BE��DE�ڵ�E.��֤:��ADC�ס�CEB.
������̽������ͼ����,����A=��B=��DEC=40��,���жϵ�E�Ƿ����ı���ABCD�ı�AB�ϵ����Ƶ�,��˵������.
������̽������ͼ��,AD��BC,DPƽ�֡�ADC,CPƽ�֡�BCD��DP�ڵ�P,����P��AB��AD�ڵ�A,��BC�ڵ�B.
(1)��֤����P���ı���ABCD�ı�AB�ϵ�һ��ǿ���Ƶ�.
(2)��AD=3,BC=5,����AB�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
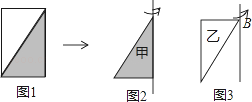
����Ŀ����ͼ1����һ�ų�10���ס���6���ij�����ֽ��ֳ�������ͬ��ֱ�������Σ�
��1���������Σ���ͼ2����תһ�ܣ������γ�һ�������ļ����壿��������Ƕ��������ף�
��2���������Σ���ͼ3����תһ�ܣ������γ�һ�������ļ����壿��������Ƕ��������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڡ�ABC�У�D��BC����һ�㣬��1=��2����3=��4.
��1������1=35�㣬���DAC�Ķ�����
��2������BAC=69�㣬���DAC�Ķ���.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com