
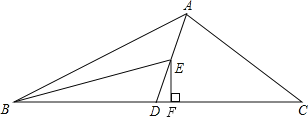
 【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?

【答案】(1)50°;(2)答案见解析;(3)6.
【解析】
试题分析:(1)根据∠BED是△ABE的一个外角得出答案;(2)根据高线的作法得出答案;(3)根据AD为△ABC的中线,BE为三角形ABD中线得出△BED的面积,然后根据等面积法求出EF的长度,从而得出点E到BC边的距离.
试题解析:(1)∵∠BED是△ABE的一个外角, ∴∠BED=∠ABE+∠BAD=15°+35°=50°.
(2)如图所示,EF即是△BED中BD边上的高.
(3)∵AD为△ABC的中线,BE为三角形ABD中线, ∴S△BED=![]() S△ABC=
S△ABC=![]() ×60=15; ∵BD=5,
×60=15; ∵BD=5,
∴EF=2S△BED÷BD=2×15÷5=6, 即点E到BC边的距离为6.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】某地计划用120~180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万立方米.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万立方米)之间的函数关系式,并给出自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石方比原计划多5000立方米,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少万立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
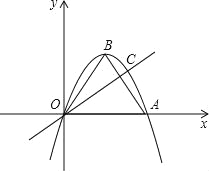
【题目】如图,在平面直角坐标系中,点O是原点,点A的坐标为(4,0),以OA为一边,在第一象限作等边△OAB
(1)求点B的坐标;
(2)求经过O、A、B三点的抛物线的解析式;
(3)直线y=![]() x与(2)中的抛物线在第一象限相交于点C,求点C的坐标;
x与(2)中的抛物线在第一象限相交于点C,求点C的坐标;
(4)在(3)中,直线OC上方的抛物线上,是否存在一点D,使得△OCD的面积最大?如果存在,求出点D的坐标和面积的最大值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
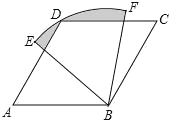
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
A.![]() ﹣
﹣![]() B.
B.![]() ﹣
﹣![]()
C.π﹣![]() D.π﹣
D.π﹣![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com