
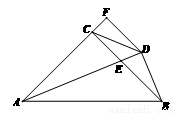
如图,在△ABC中,AC=BC,∠ ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:
①∠ADC=45°;
②BD=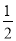 AE;
AE;
③AC+CE=AB;
④AB—BC=2FC;
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
D
【解析】
试题分析:过点E作EQ⊥AB于Q,∵∠ACB=90°,AE平分∠CAB,∴CE=EQ,∵∠ACB=90°,AC=BC ∴∠CBA=∠CAB=45° ∵EQ⊥AB ∴∠EQA=∠EQB=90° 由勾股定理可得AC=AQ ∴∠QEB=45°=∠CBA
∴EQ=BQ ∴AB=AQ+BQ=AC+CE ∴③正确
作∠ACN=∠BCD,交AD于N,∵∠CAD=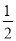 ∠CAB=22.5°=∠BAD ∴∠ABD=67.5° ∴∠DBC=22.5°=∠CAD
∠CAB=22.5°=∠BAD ∴∠ABD=67.5° ∴∠DBC=22.5°=∠CAD
∴∠DBC=∠CAD ∵AC=BC ∠ACN=∠DCB ∴△ACN≌△BCD ∴CN=CD AN=BD ∵∠ACN+∠NCE=90°
∴∠NCB+∠BCD=90° ∴∠CND=∠CDA=45° ∴∠ACN=22.5°=∠CAN ∴AN=CN ∴∠NCE=∠AEC=67.5°
∴CN=NE ∴CD-AN=EN=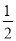 AE ∵AN=BD ∴BD=
AE ∵AN=BD ∴BD=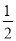 AE ∴①正确 ②正确.
AE ∴①正确 ②正确.
过D作DH⊥AB于H,∵∠FCD=∠CAD+∠CDA=67.5° ∠DBA=90°-∠DAB=67.5° ∴∠FCD=∠DBA
∵AE平分∠CAB DF⊥AC,DH⊥AB,∴DF=DH ∴△DCF≌△DBH ∴BH=CF 由勾股定理可得:AF=AH
∴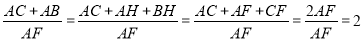 ,∴AC+AB=2AF AC+AB=2AC+2CF
,∴AC+AB=2AF AC+AB=2AC+2CF
AB-AC=2CF ∵AC=CB ∴AB-CB=2CF ∴④正确.
考点:三角形全等的判定及性质、勾股定理.


科目:初中数学 来源:2014-2015学年福建省南平市水东学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
(12分)已知:Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC,CB(或它们的延长线)于E、F,当∠EDF绕D点旋转到DE⊥AC于E时(如图1),
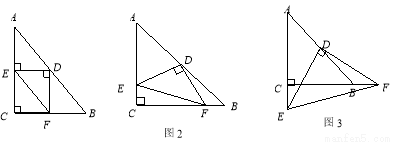
(1)易证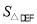 +
+ =
=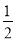
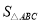 .
.
(2)当∠EDF绕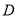 点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,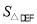 、
、 、
、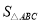 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城鞍湖实验学校八年级下学期开学检测数学试卷(解析版) 题型:解答题
(本题10分)如图,在平面直角坐标系中,A(-1,5),B (-1,0),C (-4,3).

(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1、B1、C1的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城鞍湖实验学校八年级下学期开学检测数学试卷(解析版) 题型:填空题
函数y=kx+b(k≠0)的图象平行于直线y=2x+3,且交y轴于点(0,-1),则其函数表达式是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城鞍湖实验学校八年级下学期开学检测数学试卷(解析版) 题型:选择题
下列事件是必然发生事件的是( )
A.打开电视机,正在转播足球比赛
B.小麦的亩产量一定为1500千克
C.在只装有5个红球的袋中摸出1球,是红球
D.农历十五的晚上一定能看到圆月
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区八年级上学期期末考试数学试卷(解析版) 题型:解答题
已知:如图,线段AB和射线BM交于点B.

(1)利用尺规完成以下作图,并保留作图痕迹.(不要求写作法)
①在射线BM上求作一点C,使AC=AB;
②在线段AB上求作一点D,使点D到BC,AC的距离相等;
(2)在(1)所作的图形中,若∠ABM=72°,则图中与BC相等的线段是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区八年级上学期期末考试数学试卷(解析版) 题型:选择题
已知一次函数y=kx+1,y随x的增大而增大,则该函数的图象一定经过( ).
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com