
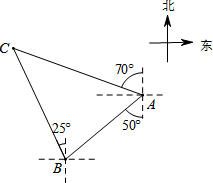
 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是| 2 |
| 3 |
| 6 |
 解:∠CBA=25°+50°=75°.
解:∠CBA=25°+50°=75°.
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 6 |


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
| 4 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
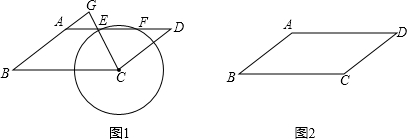
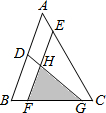 如图,点D、E、F在△ABC三边上,EF、DG相交于点H,∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=50°,图中与△GFH相似的三角形的个数是
如图,点D、E、F在△ABC三边上,EF、DG相交于点H,∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=50°,图中与△GFH相似的三角形的个数是查看答案和解析>>
科目:初中数学 来源: 题型:
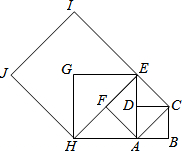 如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGF,如此下去….
如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGF,如此下去….查看答案和解析>>
科目:初中数学 来源: 题型:
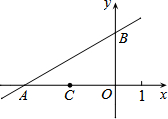 如图,在平面直角坐标系xOy中,点A(-2
如图,在平面直角坐标系xOy中,点A(-2| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com