
| 4 |
| 5 |
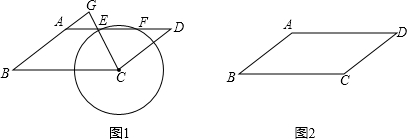
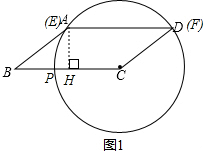 解:(1)如图1,设⊙O的半径为r,
解:(1)如图1,设⊙O的半径为r,| AH2+CH2 |
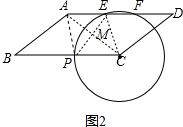
| 5 |
| 2 |
| CM |
| cos∠ACB |
| 25 |
| 8 |
(
|
| 7 |
| 4 |
| BQ |
| AB |
| 4 |
| 5 |
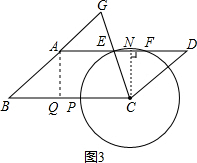
| AE |
| CB |
| AG |
| BG |
| AE |
| 8 |
| AE |
| AE+5 |
| EN2+CN2 |
| 32+12 |
| 10 |


科目:初中数学 来源: 题型:
 如图,已知二次函数y=a(x-h)2+
如图,已知二次函数y=a(x-h)2+| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
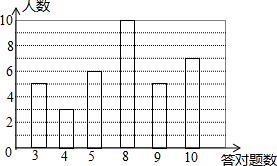 九年级一次数学模拟考试有10道选择题,抽查统计了部分学生解答这10道选择题的情况,绘制了条形统计图(如图),根据图表解答:
九年级一次数学模拟考试有10道选择题,抽查统计了部分学生解答这10道选择题的情况,绘制了条形统计图(如图),根据图表解答:查看答案和解析>>
科目:初中数学 来源: 题型:
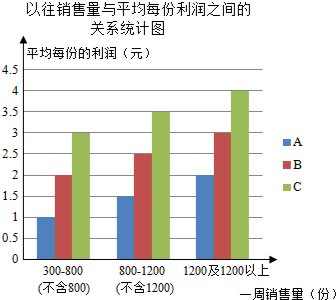 配餐公司为某学校提供A、B、C三类午餐供师生选择,三类午餐每份的价格分别是:A餐6元,B餐8元,C餐10元,为做好下阶段的营销工作,配餐公司根据该校上周A、B、C三类午餐购买情况,将所得的数据处理后,制成统计表:根据以往销售量与平均每份利润之间的关系,制成统计图(如图)
配餐公司为某学校提供A、B、C三类午餐供师生选择,三类午餐每份的价格分别是:A餐6元,B餐8元,C餐10元,为做好下阶段的营销工作,配餐公司根据该校上周A、B、C三类午餐购买情况,将所得的数据处理后,制成统计表:根据以往销售量与平均每份利润之间的关系,制成统计图(如图)| 种类 | 数量(份) |
| A | 800 |
| B | 1500 |
| C | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:
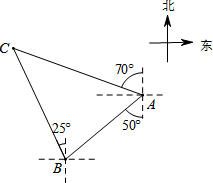 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是| 2 |
| 3 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com