
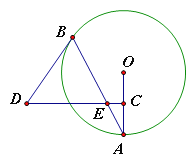
【题目】如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若CD=15,BE=10,tanA=![]() ,求⊙O的直径.
,求⊙O的直径.
【答案】(1)BD是⊙O的切线,理由见解析;(2)![]() .
.
【解析】试题分析:(1)连接OB,由已知条件易证∠OBD=90°,即可证明BD是⊙O的切线;(2)过点D作DG⊥BE于G,根据等腰三角形的性质得到EG=![]() BE=5,由两角相等的三角形相似,△ACE∽△DGE,利用相似三角形对应角相等得到sin∠EDG=sinA=
BE=5,由两角相等的三角形相似,△ACE∽△DGE,利用相似三角形对应角相等得到sin∠EDG=sinA=![]() ,在Rt△EDG中,利用勾股定理求出DG的长,根据三角形相似得到比例式,代入数据即可得到结果.
,在Rt△EDG中,利用勾股定理求出DG的长,根据三角形相似得到比例式,代入数据即可得到结果.
试题解析:(1)证明:连接OB,
∵OB=OA,DE=DB,
∴∠A=∠OBA,∠DEB=∠ABD,
又∵CD⊥OA,
∴∠A+∠AEC=∠A+∠DEB=90°,
∴∠OBA+∠ABD=90°,
∴OB⊥BD,
∴BD是⊙O的切线;
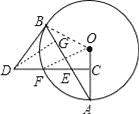
(2)如图,过点D作DG⊥BE于G,
∵DE=DB,
∴EG=![]() BE=5,
BE=5,
∵∠ACE=∠DGE=90°,∠AEC=∠GED,
∴∠GDE=∠A,
∴△ACE∽△DGE,
∴sin∠EDG=sinA=![]() =
=![]() ,即CE=13,
,即CE=13,
在Rt△ECG中,
∵DG=![]() =12,
=12,
∵CD=15,DE=13,
∴DE=2,
∵△ACE∽△DGE,
∴![]() =
=![]() ,
,
∴AC=![]() DG=
DG=![]() ,
,
∴⊙O的直径2OA=4AD=![]() .
.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】化简求值
(1)2x2﹣[x2﹣2(x2﹣3x﹣1)﹣3(x2﹣1﹣2x)],其中x= ![]()
(2)2(ab2﹣2a2b)﹣3(ab2﹣a2b)+(2ab2﹣2a2b),其中:a=3,b=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为20米,宽为12米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示: 
(1)菜地的长a=米,宽b=米;
(2)菜地的面积S=平方米;
(3)求当x=2米时,菜地的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区住宅用电之电费计算规则如下:每月每户不超过50度时,每度以4元收费;超过50度的部分,每度以5元收费,并规定用电按整数度计算(小数部份无条件舍去) .
(1)下表给出了今年3月份A,B两用户的部分用电数据,请将表格数据补充完整,
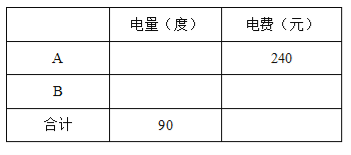
(2)若假定某月份C用户比D用户多缴电费38元,求C用户该月可能缴的电费为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点M在y轴的左侧,且在x轴的上侧,到两坐标轴的距离都是1,则点M的坐标为( )
A.(﹣1,2)
B.(﹣1,﹣1)
C.(﹣1,1)
D.(1,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com