
【题目】已知,如图△ABC中,AB=4,BC=8,D为BC边上的一点,BD=2.
(1)求证:△ABD∽△CBA;
(2)若DE∥AB交AC于点E,请你补全图形,再找出一个和△ABD相似的三角形,并计算DE的长.
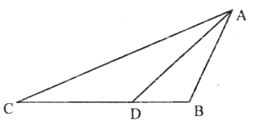
【答案】(1)证明见解析;(2)DE=3.
【解析】
(1)显然题目给出AB=4,BC=8,易得BD=8-6=2,要证△ABD∽△CBA只要证三角形中夹∠B的三角形的两条边是成比例的线段即可.
(2)根据三角形中平行线截得的三角形与原三角形相似得△CDE∽△ABC,由(1)知△ABD∽△CBA,由于相似具有传递性,所以△ABD∽△CDE;可利用相似三角形的性质:对应边成比例,从而求出DE的大小.
(1)证明:∵AB=4,BC=8,BD=2,
∴AB:CB=BD:BA.
∵∠ABD=∠CBA,
∴△ABD∽△CBA.
(2)答:△ABD∽△CDE;DE=3.

解答过程如下:△ABC中,
∵DE∥AB,
∴△CDE∽△ABC,
由(1)知△ABD∽△CBA,
∴△ABD∽△CDE,
又∵△CDE∽△ABC,
∴DE:AB=CD:BC,
DE=![]() ×AB=
×AB=![]() ×4=3.
×4=3.


科目:初中数学 来源: 题型:
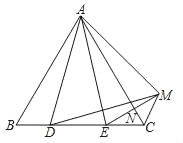
【题目】如图,△ABC是等边三角形,D,E是BC上的两点,且BD=CE,连接AD、AE,将△AEC沿AC翻折,得到△AMC,连接EM交AC于点N,连接DM.以下判断:①AD=AE,②△ABD≌△DCM,③△ADM是等边三角形,④CN=![]() EC中,正确的是_____.
EC中,正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥市拟将徽州大道南延至庐江县庐城镇,庐江段的一段土方工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该土方工程分成两部分,甲队做完其中一部分工程用了x天,乙队做完另一部分工程用了y天,若x,y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,请用含x的式子表示y,并求出两队实际各做了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
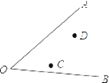
【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
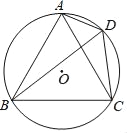
【题目】如图,四边形ABCD内接于⊙O,∠ABC=60°,BD平分∠ADC.
(1)试说明△ABC是等边三角形;
(2)若AD=2,DC=4,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
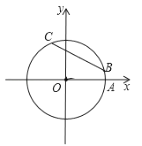
【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(![]() ,0),直线y=kx-2k+3与⊙O交于B、C两点,则弦BC的长的最小值为_______.
,0),直线y=kx-2k+3与⊙O交于B、C两点,则弦BC的长的最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
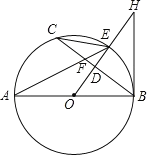
【题目】如图,AB为⊙O的直径,OD⊥弦BC于点D,交⊙O于点E,AE与BC交于点F,点H为OD延长线上一点,且∠OHB=∠AEC.
(1)求证:BH是⊙O的切线;
(2)求证:CE2=EF·EA;
(3)若⊙O的半径为5,sin∠C=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com