
 ���ⱳ�����ڡ�ABC�У�AB��BC��AC���ߵij��ֱ�Ϊ$\sqrt{5}$��$\sqrt{10}$��$\sqrt{13}$������������ε�������Ѽ�ͬѧ�ڽ�������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л�������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ����ʾ�������������ABC�ĸߣ�������������ܼ�������������
���ⱳ�����ڡ�ABC�У�AB��BC��AC���ߵij��ֱ�Ϊ$\sqrt{5}$��$\sqrt{10}$��$\sqrt{13}$������������ε�������Ѽ�ͬѧ�ڽ�������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л�������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ����ʾ�������������ABC�ĸߣ�������������ܼ����������������� ��1����һ�����ε�����ֱ��ȥ���������ε�����������ABC�������
��2�����ù��ɶ����������ص�ֱ���DEF��Ȼ����ݹ��ɶ������涨��֤����������Ϊֱ�������Σ�
���  �⣺��1����ABC�����=3��3-$\frac{1}{2}$��1��3-$\frac{1}{2}$��2��1-$\frac{1}{2}$��2��3=$\frac{7}{2}$��
�⣺��1����ABC�����=3��3-$\frac{1}{2}$��1��3-$\frac{1}{2}$��2��1-$\frac{1}{2}$��2��3=$\frac{7}{2}$��
�ʴ�Ϊ$\frac{7}{2}$��
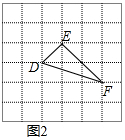
��2����ͼ2����DEFΪ������
��DEFΪֱ�������Σ��������£�
��DE=$\sqrt{2}$��EF=$\sqrt{8}$��DF=$\sqrt{10}$��
��DE2+EF2=DF2��
���DEFΪֱ�������Σ�
���� ���⿼������ͼ-������ͼ��������ͼ�������ֻ�����ͼ�Ļ����Ͻ�����ͼ��һ���ǽ���˼���ͼ�ε����ʺͻ�����ͼ���������������Ŀ�Ĺؼ�����Ϥ��������ͼ�ε����ʣ���ϼ���ͼ�εĻ������ʰѸ�����ͼ���ɻ�����ͼ��������Ҳ�����˹��ɶ������涨����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����?ABCD�У�BC=12cm����ABC=60�㣬AC��AB��O��AC���е㣬��E��F�ֱ�ӵ�O������������OA��OC�����ƶ����ٶȶ���ÿ��1cm��
��ͼ����?ABCD�У�BC=12cm����ABC=60�㣬AC��AB��O��AC���е㣬��E��F�ֱ�ӵ�O������������OA��OC�����ƶ����ٶȶ���ÿ��1cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��105 | B�� | 20��104 | C�� | 0.2��106 | D�� | 2��106 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ����C���߶�AB�ϣ���M��N�ֱ���AC��BC���е㣮
��֪����ͼ����C���߶�AB�ϣ���M��N�ֱ���AC��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a$��-\frac{1}{4}$��a��0 | B�� | a$��-\frac{1}{4}$ | C�� | a$��-\frac{1}{4}$ | D�� | a$��-\frac{1}{4}$��a��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+a4=2a2 | B�� | 3a2-2a2=1 | C�� | 3a-a=3 | D�� | 3a2-4a2=-a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2•x2=2x4 | B�� | ��-2a��3=-8a3 | C�� | ��a3��-2=a-5 | D�� | m3��m3=m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com