
【题目】甲、乙两名队员参加射击训练,成绩分别被作成下列两个统计图:
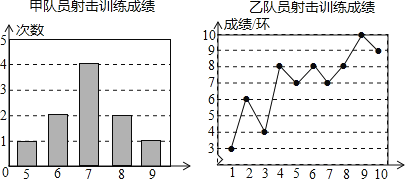
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | 7 | 7 | 1.2 | |
乙 | 7 | 8 |
(1)请计算甲的平均成绩,乙的训练成绩的中位数和方差;(列式解答)
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
【答案】(1)甲的平均成绩为7环,乙射击成绩的中位数为7.5环,方差为![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)利用平均数的计算公式直接计算平均成绩;将乙的成绩从小到大重新排列,根据中位数的定义可求出中位数;根据乙的平均数,利用方差的公式计算即可;
(2)比较平均数和方差,若平均数一样,选派方差小的队员.
解:(1)甲的平均成绩![]() (环),
(环),
∵乙射击的成绩从小到大重新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数![]() (环),
(环),
其方差![]()
![]()
![]()
(2)答:从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定;
综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.


科目:初中数学 来源: 题型:
【题目】下面是小丁设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程.
已知:如图,在RtΔABC中,∠ABC=90°,0为AC的中点.
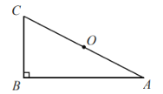
求作:四边形ABCD,使得四边形ABCD为矩形.
作法:①作射线BO,在线段BO的延长线上取点D,使得DO=BO;
②连接AD,CD,则四边形ABCD为矩形.
根据小丁设计的尺规作图过程.
(1)使用直尺和圆规,在图中补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∴点O为AC的中点,
∴AO=CO.
又∵DO=BO,
∵四边形ABCD为平行四边形(__________)(填推理的依据).
∵∠ABC=90°,
∴![]() ABCD为矩形(_________)(填推理的依据).
ABCD为矩形(_________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
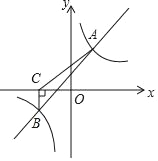
【题目】如图所示,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,4),B(﹣4,n)两点.
的图象交于A(2,4),B(﹣4,n)两点.
(1)分别求出一次函数与反比例函数的表达式;
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
社会消费品零售总额是指批发和零售业,住宿和餐饮业以及其他行业直接售给城乡居民和社会集团的消费品零售额,在各类与消费有关的统计数据中,社会消费品零售总额是表现国内消费需求最直接的数据.
2012年,北京市全年实现社会消费品零售总额7702.8亿元,比上一年增长11.6%,2013年,全年实现社会消费品零售总额8375.1亿元,比上一年增长8.7%,2014年,全年实现社会消费品零售总额9098.1亿元,比上一年增长8.6%,2015年,全年实现社会消费品零售总额10338亿元,比上一年增长7.3%.
2016年,北京市实现市场总消费19926.2亿元,比上一年增长了8.1%,其中实现服务性消费8921.1亿元,增长10.1%;实现社会消费品零售总额11005.1亿元,比上一年增长了6.5%.
根据以上材料解答下列问题:
(1)补全统计表:
2012﹣2016年北京市社会消费品零售总额统计表
年份 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 |
社会消费品零售总额(单位:亿元) | ____ | _____ | _____ | _____ | _____ |
(2)选择适当的统计图将2012﹣2016年北京市社会消费品零售总额比上一年的增长率表示出来,并在图中表明相应数据;
(3)根据以上信息,估计2017年北京市社会消费品零售总额比上一年的增长率约为_________,你的预估理由是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
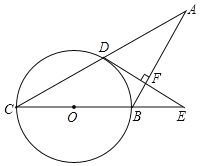
【题目】如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径R=5,tanC=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…,![]() 分裂后第一个数是____________(用含m的代数式表示);若
分裂后第一个数是____________(用含m的代数式表示);若![]() 分裂后,其中有一个奇数是2019,则m的值是_________.
分裂后,其中有一个奇数是2019,则m的值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
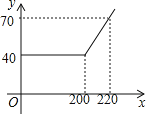
【题目】某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.
(1)当x≥200时,求y与x之间的函数关系式
(2)若小刚家10月份上网180小时,则他家应付多少元上网费?
(3)若小明家10月份上网费用为52元,则他家该月的上网时间是多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC 中,a、b、c分别为∠A、∠B、∠C的对边,则下列条件中:①a=4,b=7![]() ;c=8
;c=8![]() ;②a2:b2:C2=1:3:2;③∠A:∠B:∠C=3:4:5;④∠A=2∠B=2∠C.其中能判断△ABC是直角三角形的有( )个.
;②a2:b2:C2=1:3:2;③∠A:∠B:∠C=3:4:5;④∠A=2∠B=2∠C.其中能判断△ABC是直角三角形的有( )个.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小方家住户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区城铺设地砖.
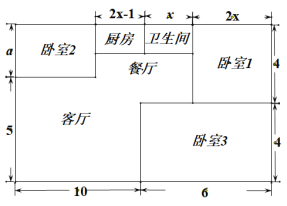
(1)求a的值.
(2)铺设地面需要木地板和地砖各多少平方米(用含![]() 的代数式表示)?
的代数式表示)?
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米,装修公司有![]() 两种活动方案,如表:
两种活动方案,如表:
活动方案 | 木地板价格 | 地砖价格 | 总安装费 |
A | 8折 | 8.5折 | 2000元 |
B | 9折 | 8.5折 | 免收 |
已知卧室2的面积是21平方米,则小方家应选择哪种活动,使铺设地面的总费用(包括材料费及安装费)更低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com