
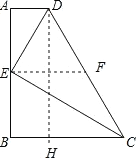
【题目】已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,![]() .E是边AB的中点,联结DE、CE,且DE⊥CE.设AD=x,BC=y.
.E是边AB的中点,联结DE、CE,且DE⊥CE.设AD=x,BC=y.
(1)如果∠BCD=60°,求CD的长;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)联结BD.如果△BCD是以边CD为腰的等腰三角形,求x的值.
【答案】(1)4; (2)x>0,且![]() ; (3)
; (3)![]()
【解析】(1)首先过点D作DH⊥BC,垂足为点H,由AD∥BC,AB⊥BC,DH⊥BC,可求得DH的长,然后设CH=x,则 CD=2x,利用勾股定理即可求得方程:x2+(2![]()
![]() )2=4x2,解此方程即可求得答案;
)2=4x2,解此方程即可求得答案;
(2)首先取CD的中点F,连接EF,由梯形的中位线,可表示出EF的长,易得四边形ABHD是平行四边形,然后由勾股定理可得:(y﹣x)2+12=(x+y)2,继而求得答案;
(3)分别从CD=BD或CD=BC去分析求解即可求得答案.
解:(1)过点D作DH⊥BC,垂足为点H.
∵AD∥BC,AB⊥BC,DH⊥BC,
∴DH=AB=2![]() ,
,
在Rt△DHC中,
∵∠BCD=60°,
∴∠CDH=30°.
∴CD=2CH,
设CH=x,则 CD=2x.
利用勾股定理,得 CH2+DH2=CD2.
即得:x2+(2![]() )2=4x2.
)2=4x2.
解得 x=2(负值舍去).
∴CD=4;
(2)取CD的中点F,连接EF,
∵E为边AB的中点,
∴EF=![]() (AD+BC)=
(AD+BC)=![]() (x+y).
(x+y).
∵DE⊥CE,
∴∠DEC=90°.
又∵DF=CF,
∴CD=2EF=x+y.
由AB⊥BC,DH⊥BC,得∠B=∠DHC=90°.
∴AB∥DH.
又∵AB=DH,
∴四边形ABHD是平行四边形.
∴BH=AD=x.
即得 CH=|y﹣x|,
在Rt△DHC中,利用勾股定理,得 CH2+DH2=CD2.
即得 (y﹣x)2+12=(x+y)2.
解得![]() ,
,
∴所求函数解析式为![]() .
.
自变量x的取值范围是x>0,且![]() ;
;
(3)当△BCD是以边CD为腰的等腰三角形时,有两种可能情况:CD=BD或CD=BC.
( i)如果CD=BD,由DH⊥BC,得 BH=CH.即得 y=2x.
利用![]() ,得
,得![]() .
.
解得![]() ,
,![]() .
.
经检验:![]() ,
,![]() ,且
,且![]() 不合题意,舍去.
不合题意,舍去.
∴![]() ;
;
( ii)如果CD=BC,则 x+y=y.
即得 x=0(不合题意,舍去),
综上可得:![]() .
.
“点睛”此题属于四边形的综合题.考查了梯形的性质、平行四边形的判定与性质、等腰三角形的性质以及勾股定理等知识.注意掌握辅助线的作法,掌握方程思想与分类讨论思想的应用是解此题的关键.


科目:初中数学 来源: 题型:
【题目】不能使两个直角三角形全等的条件是( ).
A.一条直角边及其对角对应相等B.斜边和两条直角边对应相等
C.斜边和一条直角边对应相等D.两个锐角对应相等
查看答案和解析>>
科目:初中数学 来源: 题型:
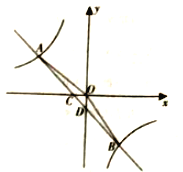
【题目】(2016重庆市第22题)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与Y轴交于点D,点B的坐标为(m,-4),连接AO,AO=5,sin∠AOC=![]() 。
。
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级社会实践小组去商场调查商品销售情况,了解到该商场以每件80元的价格购进了某品牌衬衫500件,并以每件120元的价格销售了400件,商场准备采取促销措施,将剩下的衬衫降价销售.请你帮商场计算一下,每件衬衫降价多少元时,销售完这批衬衫正好达到盈利45%的预期目标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=8,AD=4.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为x(秒),在整个运动过程中,当△APQ为直角三角形时,则相应的x的值或取值范围是_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在□ABCD中,E为边CD的中点,联结AE并延长,交边BC的延长线于点F.
(1)求证:四边形ACFD是平行四边形;
(2)如果∠B+∠AFB=90°,求证:四边形ACFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个数用大括号括起来,相邻两个数之间用逗号隔开,如: ![]() ,
, ![]() ,...,我们称之为集合,其中每一个数称为该集合的元素.如果一个所有元素均为有理数的集合满足:当有理数
,...,我们称之为集合,其中每一个数称为该集合的元素.如果一个所有元素均为有理数的集合满足:当有理数![]() 是集合的一个元素时,
是集合的一个元素时,![]() 也必是这个集合的元素,这样的集合我们又称为黄金集合.例如,
也必是这个集合的元素,这样的集合我们又称为黄金集合.例如, ![]() 就是一个黄金集合.
就是一个黄金集合.
(1)集合![]() ______黄金集合,集合
______黄金集合,集合![]() _______黄金集合;(填“是”或“不是”)
_______黄金集合;(填“是”或“不是”)
(2)若一个黄金集合中最大的一个元素为![]() ,则该集合是否存在最小的元素?如果存在,请直接写出答案,否则说明理由.
,则该集合是否存在最小的元素?如果存在,请直接写出答案,否则说明理由.
(3)若一个黄金集合中所有元素之和为整数![]() ,且
,且![]() ,则该黄金集合中共有多少个元素?请说明你的理由.
,则该黄金集合中共有多少个元素?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某鞋店先后卖出7双某品牌的运动鞋,其尺码依次为(单位:码):40,39,40,41,42,41,41,则这组数据的众数是( )
A. 39 B. 40 C. 41 D. 42
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com