
【题目】某中学七年级开设了艺术课程,每名学生从合唱、管弦乐、舞蹈、动漫、吉他这五门课程中选择一门进行学习.为了解学生的选择意向,从七年级随机抽取了若干名同学进行了调查,将调查得到的结果绘制成如图所示的两幅统计图(均不完整).
根据题中信息,回答下列问题:
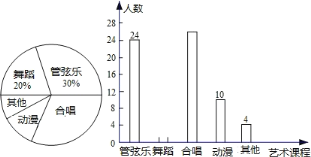
(1)在这次调查中,一共抽取了多少名学生?
(2)补全条形统计图;
(3)若该校七年级一共有 240 名学生,请估计其中有多少人会选择合唱课程.
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于二、四象限内的
的图象交于二、四象限内的![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
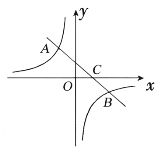
(1)求该反比例函数和一次函数的解析式;
(2)连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(3)设点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() 是直角三角形,直接写出点
是直角三角形,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A是![]() 上一动点,D是弦BC上一定点,连接AB,AC,AD.设线段AB的长是xcm,线段AC的长是
上一动点,D是弦BC上一定点,连接AB,AC,AD.设线段AB的长是xcm,线段AC的长是![]() cm,线段AD的长是
cm,线段AD的长是![]() cm.
cm.
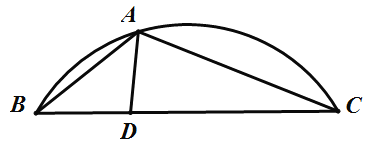
小腾根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化的关系进行了探究.下面是小腾的探究过程,请补充完整:
随自变量x的变化的关系进行了探究.下面是小腾的探究过程,请补充完整:
(1)对于点A在![]() 上的不同位置,画图、测量,得到了
上的不同位置,画图、测量,得到了![]() ,
,![]() 的长度与x的几组值:
的长度与x的几组值:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | |
x/cm | 0.00 | 0.99 | 2.01 | 3.46 | 4.98 | 5.84 | 7.07 | 8.00 |
| 8.00 | 7.46 | 6.81 | 5.69 | 4.26 | 3.29 | 1.62 | 0.00 |
| 2.50 | 2.08 | 1.88 | 2.15 | 2.99 | 3.61 | 4.62 | m |
请直接写出上表中的m值是 ;
(2)在同一平面直角坐标系![]() 中,描出补全后表中各组数据所对应的点(x,
中,描出补全后表中各组数据所对应的点(x,![]() ),(x,
),(x,![]() ),并画出函数
),并画出函数![]() ,
,![]() 的图象;
的图象;
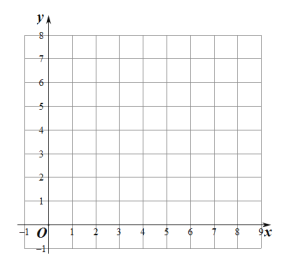
(3)结合函数图象,解决问题:当AC=AD时,AB的长度约为 cm;当AC=2AD时,AB的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A是y轴上一点,其坐标为(0,6),点B在x轴的正半轴上.点P,Q均在线段AB上,点P的横坐标为m,点Q的横坐标大于m,在△PQM中,若PM∥x轴,QM∥y轴,则称△PQM为点P,Q的“肩三角形.
(1)若点B坐标为(4,0),且m=2,则点P,B的“肩三角形”的面积为 ;
(2)当点P,Q的“肩三角形”是等腰三角形时,求点B的坐标;
(3)在(2)的条件下,作过O,P,B三点的抛物线y=ax2+bx+c
①若M点必为抛物线上一点,求点P,Q的“肩三角形”面积S与m之间的函数关系式,并写出自变量m的取值范围.
②当点P,Q的“肩三角形”面积为3,且抛物线y=ax2+bx+c与点P,Q的“肩三角形”恰有两个交点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
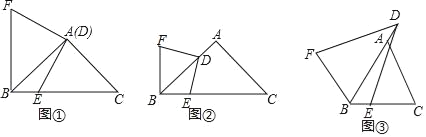
【题目】观察猜想:(1)如图①,在Rt△ABC中,∠BAC=90°,AB=AC=3,点D与点A重合,点E在边BC上,连接DE,将线段DE绕点D顺时针旋转90°得到线段DF,连接BF,BE与BF的位置关系是 ,BE+BF= ;
探究证明:(2)在(1)中,如果将点D沿AB方向移动,使AD=1,其余条件不变,如图②,判断BE与BF的位置关系,并求BE+BF的值,请写出你的理由或计算过程;
拓展延伸:(3)如图③,在△ABC中,AB=AC,∠BAC=a,点D在边BA的延长线上,BD=n,连接DE,将线段DE绕着点D顺时针旋转,旋转角∠EDF=a,连接BF,则BE+BF的值是多少?请用含有n,a的式子直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
港珠澳大桥是世界上最长的跨海大桥,是被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.开通后从香港到珠海的车程由原来的180千米缩短到50千米,港珠澳大桥的设计时速比按原来路程行驶的平均时速多40千米,若开通后按设计时速行驶,行驶完全程时间仅为原来路程行驶完全程时间的![]() ,求港珠澳大桥的设计时速是多少.
,求港珠澳大桥的设计时速是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数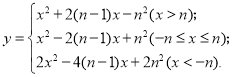 其中
其中![]() 是常数,且
是常数,且![]() >0.
>0.
(1)若点(![]() ,2)在函数的图象上,求
,2)在函数的图象上,求![]() 的值.
的值.
(2)当![]() =1时,①当
=1时,①当![]() ≤
≤![]() ≤2时,求函数值
≤2时,求函数值![]() 的取值范围.
的取值范围.
②当![]() ≤
≤![]() ≤
≤![]() 时,函数图象上的点到
时,函数图象上的点到![]() 轴的距离恒(永远)小于6,求
轴的距离恒(永远)小于6,求![]() 的取值范围.
的取值范围.
(3)直接写出函数图象与![]() 有两个交点时的
有两个交点时的![]() 取值范围.
取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
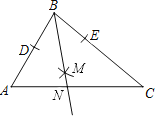
【题目】如图,在△ABC中,按以下步骤作图:①以B为圆心,任意长为半径作弧,交AB于D,交BC于E;②分别以D,E为圆心,以大于![]() DE的同样长为半径作弧,两弧交于点M;③作射线BM交AC于N.如果BN=NC,∠A=57°,那么∠ABN的度数为_____.
DE的同样长为半径作弧,两弧交于点M;③作射线BM交AC于N.如果BN=NC,∠A=57°,那么∠ABN的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
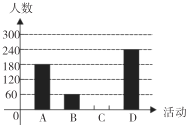
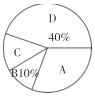
【题目】为了丰富居民的文化生活.某社区开展跳舞、绘画、游泳、唱歌等活动来让居民娱乐.为了解居民对跳舞、绘画、游泳、唱歌这四种活动(以下分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示这四种不同活动)的喜爱情况,在“五一”劳动节期间对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.请根据以上信息回答:
表示这四种不同活动)的喜爱情况,在“五一”劳动节期间对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将不完整的条形图补充完整;
(3)若居民区有8000人,请估计爱唱歌的人数?
(4)在“五—”劳动节期间,该社区针对跳舞、绘画、游泳、唱歌起带头作用的居民各选举一名进行奖励,同时随机抽取两人进行现场展示,请用列表或画树状图法求恰好选中跳舞和绘画的概率.(跳舞、绘画、游泳、唱歌分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示)
表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com