
����Ŀ����ͼ������QPN�Ķ���P��������ABCD�����Խ��ߵĽ��㴦����QPN=��������QPN�Ƶ�P��ת����ת��������QPN�����߷ֱ���������ABCD�ı�AD��CD���ڵ�E�͵�F����F���C��D���غϣ���
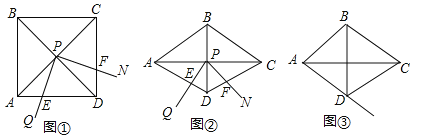
��1����ͼ�٣�����=90��ʱ��DE��DF��AD֮�������������ϵ�� ��
��2����ͼ�ڣ���ͼ���е�������ABCD��Ϊ��ADC=120������Σ������������䣬����=60��ʱ����1���еĽ��۱�ΪDE+DF=![]() AD�������֤����
AD�������֤����
��3���ڣ�2���������£�����ת��������QPN�ı�PQ������AD���ڵ�E�������������䣬̽���������˶��仯�����У�DE��DF��AD֮�������������ϵ��ֱ��д�����ۣ����ü���֤����
���𰸡���1��DE+DF=AD����2��֤���������������3���ٵ���E����AD��ʱ��DE+DF=![]() AD���ڵ���E����AD���ӳ�����ʱ��DF��DE =
AD���ڵ���E����AD���ӳ�����ʱ��DF��DE =![]() AD��
AD��
��������
�����������1��֤����APE�ա�DPF���õ�AE=DF�����ɵó�����DE+DF=AD��
��2��ȡAD���е�M������PM����֤����MDP�ǵȱ������Σ���MPE�ա�FPD������ME=DF����DE+ME=![]() AD�����ɵó�DE+DF=
AD�����ɵó�DE+DF=![]() AD��
AD��
��3���ٵ���E����AD��ʱ��DE+DF=![]() AD���ڵ���E����AD���ӳ�����ʱ��DF��DE =
AD���ڵ���E����AD���ӳ�����ʱ��DF��DE =![]() AD��
AD��
�����������1��������ABCD�ĶԽ���AC��BD���ڵ�P����PA=PD����PAE=��PDF=45�㣬�ߡ�APE+��EPD=��DPF+��EPD=90�㣬���APE=��DPF������APE����DPF�����ߡ�APE=��DPF��PA=PD����PAE=��PDF�����APE�ա�DPF��ASA������AE=DF����DE+DF=AD��
��2����ͼ�ڣ�ȡAD���е�M������PM�����ı���ABCDΪ��ADC=120������Σ���BD=AD����DAP=30�㣬��ADP=��CDP=60�㣬���MDP�ǵȱ������Σ���PM=PD����PME=��PDF=60�㣬�ߡ�PAM=30�㣬���MPD=60�㣬�ߡ�QPN=60�㣬���MPE=��FPD������MPE����FPD�У��ߡ�PME=��PDF��PM=PD����MPE=��FPD�����MPE�ա�FPD��ASA������ME=DF����DE+DF=![]() AD��
AD��

��3����ͼ���������˶��仯�����У��ٵ���E����AD��ʱ��DE+DF=![]() AD��
AD��
�ڵ���E����AD���ӳ�����ʱ��DF��DE =![]() AD��
AD��
����ͼ3��ȡAD�е�M������PM��֤����MPE�ա�DPF��


 �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������вμ��п���������Լ��41300�ˣ���41300�ÿ�ѧ��������ʾΪ�� ��
A.413��102
B.41.3��103
C.4.13��104
D.0.413��103
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1������
��ͼ1�����ı���ABCD�У���PΪAB��һ�㣬��DPC=��A=��B=90�㣬��֤��ADBC=APBP��
��2��̽��
��ͼ2�����ı���ABCD�У���PΪAB��һ�㣬����DPC=��A=��B=��ʱ�����������Ƿ���Ȼ������˵�����ɣ�
��3��Ӧ��
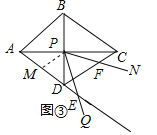
�����ã�1����2����õľ��������⣺��ͼ3���ڡ�ABD�У�AB=6��AD=BD=5����P��ÿ��1����λ���ȵ��ٶȣ��ɵ�A���ˣ��ر�AB���B�˶����������DPC=��A�����P���˶�ʱ��Ϊt���룩������DΪԲ�ģ���DCΪ�뾶��Բ��AB����ʱ����t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijѧУȫ���ְ�������Ƶ���ֲ�ֱ��ͼ��ÿ�����������Сֵ�����������ֵ��������ͼ���ṩ����Ϣ������˵���д�����ǣ� �� 
A.��ѧУ��ְ����������50��
B.��һ��������40��x��42С��Ľ�ְ������ռ��ѧУȫ���ְ����������20%
C.��ְ���������λ��һ������40��x��42��һ��
D.��ְ�����������һ����38��x��40��һ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ����( )
A. �ӳ��߶�AB���ӳ��߶�BA�ĺ�����ͬ
B. ����AB������BA��ͬһ������
C. ����������Ի�һ��ֱ�ߣ�����ֻ�ܻ�һ��ֱ��
D. �ӳ�ֱ��AB
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ���ı���ABCD����������ȷ����( )
A. ��AB��BC����ƽ���ı���ABCD������ B. ��AC��BD����ƽ���ı���ABCD��������
C. ��AC=BD����ƽ���ı���ABCD�Ǿ��� D. ��AB=AD,��ƽ���ı���ABCD��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɲ����ľ���y����λ��m������ʻ��ʱ��x����λ��s���ĺ�����ϵʽ�ǣ�y��10x��x2����ô����ɲ����ֹ������_____m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ο����У�ij�༶����ѧ�ɼ�ͳ��ͼ���£�����˵��������ǣ� �� 
A.�÷���70��80��֮����������
B.�ð��������Ϊ40
C.�÷���90��100��֮�����������
D.����60�֣�������26
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���D��E��F�ֱ���AB��BC��AC�ϣ��ҡ�ADF+��DEC=180�㣬��AFE=��BDE��
��1����ͼ1����DE=DFʱ��ͼ1���Ƿ������AB��ȵ��߶Σ������ڣ����ҳ���������֤�����������ڣ�˵�����ɣ�
��2����ͼ2����DE=kDF������0��k��1��ʱ������A=90�㣬AF=m����BD�ij����ú�k��m��ʽ�ӱ�ʾ����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com