
【题目】(1)问题
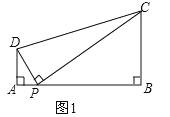
如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°,求证:ADBC=APBP.
(2)探究
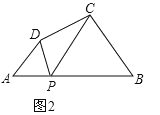
如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用
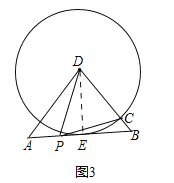
请利用(1)(2)获得的经验解决问题:如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出了,沿边AB向点B运动,且满足∠DPC=∠A,设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切时,求t的值.

【答案】(1)证明见试题解析;(2)成立,理由见试题解析;(3)1或5.
【解析】
试题分析:(1)如图1,由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC,即可证到△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(2)如图2,由∠DPC=∠A=∠B=θ可得∠ADP=∠BPC,即可证到△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(3)如图3,过点D作DE⊥AB于点E,根据等腰三角形的性质可得AE=BE=3,根据勾股定理可得DE=4,由题可得DC=DE=4,则有BC=5﹣4=1.易证∠DPC=∠A=∠B.根据ADBC=APBP,就可求出t的值.
试题解析:(1)如图1,∵∠DPC=∠A=∠B=90°,∴∠ADP+∠APD=90°,∠BPC+∠APD=90°,∴∠ADP=∠BPC,∴△ADP∽△BPC,∴![]() ,∴ADBC=APBP;
,∴ADBC=APBP;
(2)结论ADBC=APBP仍然成立.理由:如图2,
∵∠BPD=∠DPC+∠BPC,∠BPD=∠A+∠ADP,∴∠DPC+∠BPC=∠A+∠ADP,∵∠DPC=∠A=∠B=θ,∴∠BPC=∠ADP,∴△ADP∽△BPC,∴![]() ,∴ADBC=APBP;
,∴ADBC=APBP;
(3)如图3,过点D作DE⊥AB于点E.∵AD=BD=5,AB=6,∴AE=BE=3,由勾股定理可得DE=4,∵以点D为圆心,DC为半径的圆与AB相切,∴DC=DE=4,∴BC=5﹣4=1,又∵AD=BD,∴∠A=∠B,∴∠DPC=∠A=∠B,由(1)、(2)的经验可知ADBC=APBP,∴5×1=t(6﹣t),解得:![]() ,
,![]() ,∴t的值为1秒或5秒.
,∴t的值为1秒或5秒.


科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F. 
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民月用水量,某市对某区居民用水量进行了抽样调查,并制成如下直方图.
(1)这次一共抽查了户;
(2)用水量不足10吨的有户,用水量超过16吨的有户;
(3)假设该区有8万户居民,估计用水量少于10吨的有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
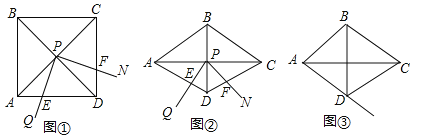
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是 ;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=![]() AD,请给出证明;
AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com