【题目】如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．
（1）求证：DE=DF；
（2）若∠A=60°，BE=1，求△ABC的周长．

参考答案：

【答案】
（1）证明：∵DE⊥AB，DF⊥AC，

∴∠BED=∠CFD=90°，

∵AB=AC，

∴∠B=∠C（等边对等角）．

∵D是BC的中点，

∴BD=CD．

在△BED和△CFD中，

，

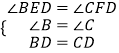∴△BED≌△CFD（AAS）．

∴DE=DF


（2）解：∵AB=AC，∠A=60°，

∴△ABC为等边三角形．

∴∠B=60°，

∵∠BED=90°，

∴∠BDE=30°，

∴BE= BD，

∵BE=1，

∴BD=2，

∴BC=2BD=4，

∴△ABC的周长为12


【解析】（1）根据DE⊥AB，DF⊥AC，AB=AC，求证∠B=∠C．再利用D是BC的中点，求证△BED≌△CFD即可得出结论．（2）根据AB=AC，∠A=60°，得出△ABC为等边三角形．然后求出∠BDE=30°，再根据题目中给出的已知条件即可算出△ABC的周长．

关闭