
【题目】如图,直线y=ax+b(a≠0)的图象与x轴、y轴分别交于点B、C,与反比例函数y=![]()
![]() (m>0)分别交于点A、B.已知A(﹣8,y0),D(x0,4),tan∠BOA=
(m>0)分别交于点A、B.已知A(﹣8,y0),D(x0,4),tan∠BOA=![]()
(1)求反比例函数和一次函数的解析式;
(2)求△BOD的面积

【答案】(1) y=0.5x+3;(2)12
【解析】
(1)根据tan∠BOA=![]() ,A(﹣8,y0),可求得y0=﹣1,从而可得点A坐标,利用待定系数法可求得反比例函数的解析式为y=
,A(﹣8,y0),可求得y0=﹣1,从而可得点A坐标,利用待定系数法可求得反比例函数的解析式为y=![]() ,继而可求得点D坐标,根据点A、点D坐标利用待定系数法即可求得一次函数的解析式;
,继而可求得点D坐标,根据点A、点D坐标利用待定系数法即可求得一次函数的解析式;
(2)根据一次函数解析式求得B点坐标,结合D点坐标利用三角形面积公式进行求解即可得.
(1)∵tan∠BOA=![]() ,A(﹣8,y0),
,A(﹣8,y0),
∴﹣![]() ,
,
y0=﹣1,
点A的坐标为(﹣8,﹣1),
把点A(﹣8,﹣1)代入y=![]() 得:
得:
﹣1=![]() ,
,
解得:m=8,
即反比例函数的解析式为y=![]() ,
,
把点D(x0,4)代入反比例函数y=![]() 得:
得:![]() =4,
=4,
解得:x0=2,
即点D的坐标为(2,4),
把A(﹣8,﹣1)和D(2,4)代入y=ax+b得:
![]() ,
,
解得:![]() ,
,
即一次函数的解析式为:y=0.5x+3;
(2)把y=0代入y=0.5x+3得:x=﹣6,
即点B的坐标为(﹣6,0),
OB=6,
S△BOD=![]() =12,
=12,
即△BOD的面积为12.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
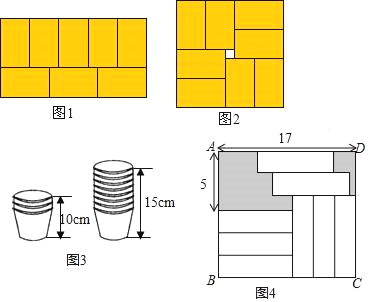
小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:
(1)请按照小明的思路完成上述问题:求每个小长方形的面积;
(2)某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是 cm;
(3)小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面坐标系中,ΔABC是等腰直角三角形,∠ABC=90°,AB=BC,点A坐标为(-8,-3),点B坐标为(0,-5),AC交x轴于点D.

(1)求点C和D的坐标;
(2)点M在x轴上,当ΔAMB的周长最小时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点 A1,A2,A3…在射线ON 上,点B1,B2,B3…在射线OM 上,△A1B1A2,△A2B3A3,△A3B3A4![]() 均为等边三角形,若OA1=2,则△A7B7A8 的边长为____.
均为等边三角形,若OA1=2,则△A7B7A8 的边长为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有菱形OABC,点A的坐标为(5,0),对角线OB、AC相交于点D,双曲线y=![]() (x>0)经过AB的中点F,交BC于点E,且OBAC=40,有下列四个结论:
(x>0)经过AB的中点F,交BC于点E,且OBAC=40,有下列四个结论:
①双曲线的解析式为y=![]() (x>0);②直线OE的解析式为y=
(x>0);②直线OE的解析式为y=![]() x;③tan∠CAO=
x;③tan∠CAO=![]() ;④AC+OB=6
;④AC+OB=6![]() ;其中正确的结论有( )
;其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴和
轴和![]() 轴交于
轴交于![]() ,
,![]() 两点,且与正比例函数
两点,且与正比例函数![]() 的图象交于点
的图象交于点![]() .
.

(1)求![]() 的值;
的值;
(2)求正比例函数的表达式;
(3)点![]() 是一次函数图象上的一点,且
是一次函数图象上的一点,且![]() 的面积是3,求点
的面积是3,求点![]() 的坐标;
的坐标;
(4)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的值最小?若存在,求出点
的值最小?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是直线l上的三个点,∠DAB=∠DBE=∠ECB=a,且BD=BE.
(1)求证:AC=AD+CE;
(2)若a=120°,点F在直线l的上方,△BEF为等边三角形,补全图形,请判断△ACF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1个单位的正方形,A(-3,1),B(3,2),解答以下问题:
(1)在图中标出平面直角坐标系的原点O,并建立直角坐标系;
(2)点A关于x轴的对称点A’坐标为 ,并在坐标系中画出点A’;
(3)点P是x轴上一点,当PA+PB最小时,在图中画出点P的位置.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com