
【题目】如图,A、B、C是直线l上的三个点,∠DAB=∠DBE=∠ECB=a,且BD=BE.
(1)求证:AC=AD+CE;
(2)若a=120°,点F在直线l的上方,△BEF为等边三角形,补全图形,请判断△ACF的形状,并说明理由.

【答案】(1)详见解析;(2)△ACF为等边三角形.
【解析】
(1)由外角的性质可得∠ADB=∠CBE,由“AAS”可得△ADB≌△CBE,可得AD=CB,AB=CE,可得结论;
(2)由“SAS”可证△AFB≌△CFE,可得AF=CF,∠AFB=∠CFE,可得∠AFC=∠AFB+∠BFC=∠CFE+∠BFC=60°,可得△ACF是等边三角形.
证明:(1)∵∠DAB=∠DBE=α,
∴∠ADB+∠ABD=∠CBE+∠ABD=180°﹣α.
∴∠ADB=∠CBE
在△ADB和△CBE中,
∵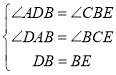 ,
,
∴△ADB≌△CBE(AAS)
∴AD=CB,AB=CE.
∴AC=AB+BC=AD+CE
(2)补全图形.
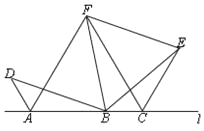
△ACF为等边三角形.
理由如下:
∵△BEF为等边三角形,
∴BF=EF,∠BFE=∠FBE=∠FEB=60°.
∵∠DBE=120°,∴∠DBF=60°.
∵∠ABD=∠CEB(已证),
∴∠ABD+∠DBF=∠CEB+∠FEB,
即∠ABF=∠CEF.
∵AB=CE(已证),
∴△AFB≌△CFE(SAS),
∴AF=CF,∠AFB=∠CFE.
∴∠AFC=∠AFB+∠BFC=∠CFE+∠BFC=60°.
∴△ACF为等边三角形.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于![]() BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )
BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )

A. ∠CAD=40° B. ∠ACD=70° C. 点D为△ABC的外心 D. ∠ACB=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+b(a≠0)的图象与x轴、y轴分别交于点B、C,与反比例函数y=![]()
![]() (m>0)分别交于点A、B.已知A(﹣8,y0),D(x0,4),tan∠BOA=
(m>0)分别交于点A、B.已知A(﹣8,y0),D(x0,4),tan∠BOA=![]()
(1)求反比例函数和一次函数的解析式;
(2)求△BOD的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夷陵区园林处为了对一段公路进行绿化,计划购买A、B两种风景树,已知若用8000元买A种树要比买B种树多买20棵,A、B两种树的相关信息如下表:
项目品种 | 单价(元/棵) | 成活率 |
A | m | 91% |
B | 100 | 97% |
(1)求表中m的值;
(2)预计对这段公路的绿化需购1000棵这样的风景树.若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A、B两种树各多少棵?最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:
①OD2=DECD;②AD+BC=CD;③OD=OC;④S梯形ABCD=![]() CDOA;⑤∠DOC=90°,
CDOA;⑤∠DOC=90°,
其中正确的是_____.(只需填上正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
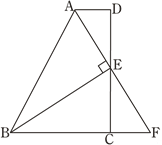
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F. 已知AD=2cm,BC=5cm.
(1)求证:FC=AD;
(2)求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为等边三角形ABC内的一点, DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD',下列结论:①点D与点D'的距离为5;②∠ADC=150°;③△ACD'可以由△ABD绕点A逆时针旋转60°得到;④点D到CD'的距离为3;⑤S四边形ABCD′=6+![]() ,其中正确的有( )
,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=![]() ,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是( )
,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是( )

A. 2 ![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com