
����Ŀ���������ִ�Ϊ�˶�һ�ι�·�����̻����ƻ�����A��B���ַ羰������֪����8000Ԫ��A����Ҫ����B��������20�ã�A��B�������������Ϣ���±���
��ĿƷ�� | ���ۣ�Ԫ/�ã� | �ɻ��� |
A | m | 91% |
B | 100 | 97% |
��1�������m��ֵ��
��2��Ԥ�ƶ���ι�·���̻��蹺1000�������ķ羰������ϣ���������ijɻ��ʲ�����94%����ʹ�������ܷ�����ͣ�Ӧѡ��A��B�����������ٿã���ͷ���Ϊ���٣�
���𰸡���1��m=80;(2) Ӧ��A����500�ã�B����500��
��������
��1�����������г��й�m�ķ��̣�![]() ���m��ֵ���ɣ�
���m��ֵ���ɣ�
��2���ȸ��ݹ������ܷ���=��A�����ķ���+��B�����ķ��ã������ó�y��x�ĺ�����ϵʽ������A�����ijɻ������+B�����ijɻ������������������ƽ���ɻ������жϳ�x��ȡֵ�������ݺ����������жϳ���ѵķ�����
(1)������8000Ԫ��A����Ҫ����B��������20�ã�
���������ã�![]()
��ã�m=80��
������m=80��ԭ���̵ĸ����ҷ������⣻
(2)�蹺��A����x�ã�����������ܷ���ΪyԪ��
���������y=80x+100(1000x)
=20x+100000��
![]()
![]()
![]()
![]()
��y=20x+100000��x�����������
�൱x=500ʱ,�����������Ϊy=20��500+100000=90000(Ԫ).
��x=500ʱ��1000x=500��
���ʱӦ��A����500�ã�B����500�á�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���ֽƬABCD����ͼ��ʽ�۵���ʹ��C��A�غϣ���D�䵽D�������ۺ�ΪEF��

��1����֤����ABE�ա�AD��F��
��2������CF���ж��ı���AECF��ʲô�����ı��Σ�֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��MON��30������ A1,A2,A3��������ON �ϣ���B1,B2,B3��������OM �ϣ���A1B1A2����A2B3A3����A3B3A4![]() ��Ϊ�ȱ������Σ���OA1=2������A7B7A8 �ı߳�Ϊ____.
��Ϊ�ȱ������Σ���OA1=2������A7B7A8 �ı߳�Ϊ____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ��ֱ���
��ͼ��ֱ���![]() ���
���![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��������������
���㣬��������������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() .
.

��1����![]() ��ֵ��
��ֵ��
��2���������������ı���ʽ��
��3����![]() ��һ�κ���ͼ���ϵ�һ�㣬��
��һ�κ���ͼ���ϵ�һ�㣬��![]() �������3�����
�������3�����![]() �����ꣻ
�����ꣻ
��4����![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ
��ʹ![]() ��ֵ��С�������ڣ������
��ֵ��С�������ڣ������![]() �����꣬�������ڣ�˵������.
�����꣬�������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ƽ��
ƽ��![]() ����
����![]() ��
��![]() ����
����![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �����н��ۣ���
�����н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() .������ȷ���ǣ� ��
.������ȷ���ǣ� ��

A.�٢�B.�٢�C.�٢ڢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABE����CDE���ǵ���ֱ�������Σ���AEB����DEC��90��������AD��AC��BC��BD����AD��AC��AB�������н��ۣ���AE��ֱƽ��CD����ACƽ����BAD���ۡ�ABD�ǵȱ������Σ��ܡ�BCD�Ķ���Ϊ150����������ȷ�ĸ����ǣ� ��

A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B��C��ֱ��l�ϵ������㣬��DAB����DBE����ECB��a����BD��BE��
��1����֤��AC��AD+CE��
��2����a��120������F��ֱ��l���Ϸ�����BEFΪ�ȱ������Σ���ȫͼ�Σ����ж���ACF����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
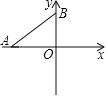
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A����4��0����B��0��3������D��y�Ḻ�����ϵ�һ�㣮����ABD�ǵ���������ʱ����D������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ![]() ������AC��BD���ڵ�O��CEƽ�֡�ACD��BD�ڵ�E��
������AC��BD���ڵ�O��CEƽ�֡�ACD��BD�ڵ�E��
��1����DE�ij���
��2������EF��EF��CE����AB�ڵ�F����BF�ij���
��3������E��EG��CE����CD�ڵ�G����DG�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com