
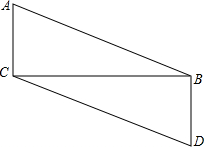
 已知:如图,AC⊥CB,BD⊥BC,AB=DC.求证:AB∥CD.
已知:如图,AC⊥CB,BD⊥BC,AB=DC.求证:AB∥CD. 科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 跑步训练量与前一天相比变化情况(米) | +100 | -20 | +50 | +20 | -35 | +15 | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
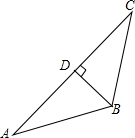 如图,在△ABC中,BD⊥AC于点D,若BC=10,AC=20,∠C=37°,求AB的长.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,在△ABC中,BD⊥AC于点D,若BC=10,AC=20,∠C=37°,求AB的长.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
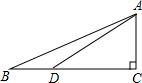 如图,AC⊥BC,cos∠ADC=$\frac{4}{5}$,tanB=$\frac{{\sqrt{3}}}{3}$,AD=10,求:(1)AC的长;(2)BD的长.
如图,AC⊥BC,cos∠ADC=$\frac{4}{5}$,tanB=$\frac{{\sqrt{3}}}{3}$,AD=10,求:(1)AC的长;(2)BD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
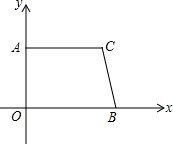 如图,在直角梯形AOBC中,AC∥OB,且OB=6,AC=5,OA=4.
如图,在直角梯形AOBC中,AC∥OB,且OB=6,AC=5,OA=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com