
【题目】在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式: ![]() =
= ![]() )( )
)( )
A.25 ![]() +75
+75
B.50 ![]() +50
+50
C.75 ![]() +75
+75
D.50 ![]() +100
+100
【答案】D
【解析】解:设AE=xm,在Rt△AEP中∠PAE=45°,则∠P=45°,
∴PE=AE=x,
∵山顶A处高出水面50m,
∴OE=50m,
∴OP′=OP=PE+OE=x+50,
∵∠P′AE=60°,
∴P′E=tan60°AE= ![]() x,
x,
∴OP′=P′E﹣OE= ![]() x﹣50,
x﹣50,
∴x+50= ![]() x﹣50,
x﹣50,
解得:x=50( ![]() +1)(m),
+1)(m),
∴PO=PE+OE=50( ![]() +1+50=50
+1+50=50 ![]() +100(m),
+100(m),
即飞艇离开湖面的高度是(50 ![]() +100)m.
+100)m.
故选D.
设AE=x,则PE=AE=x,根据山顶A处高出水面50m,得出OE=50,OP′=x+50,根据∠P′AE=60°,得出P′E= ![]() x,从而列出方程,求出x的值即可.
x,从而列出方程,求出x的值即可.


科目:初中数学 来源: 题型:
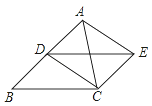
【题目】已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形,
(1)求证:四边形ADCE是平行四边形;
(2)当△ABC满足什么条件时,平行四边形ADCE是矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3 cm,以直线AB为轴,将正方形旋转一周,得到一几何体.
(1)画出从正面观察这个几何体得到的平面图;
(2)求(1)中平面图的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区举办科技比赛,某校参加科技比赛(包括电子百拼、航模、机器人、建模四个类别)的参赛人数统计图如图
(1)该校参加机器人比赛的人数是_____人;“航模”所在扇形的圆心角度数是________°;
(2)补全条形统计图;
(3)从全区参加科技比赛选手中随机抽取80人,其中有16人获奖.今年全区参加科技比赛人数共有3215人,请你估算全区参加科技比赛的获奖人数约是多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF. 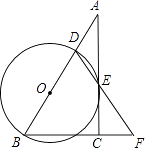
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD,已知BC=BD,AB=4,BC=2 ![]() .
. 
(1)求证:BD是⊙O的切线;
(2)求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在抗震救灾期间承担40 000顶救灾帐篷的生产任务,分为A、B、C、D四种型号,它们的数量百分比和每天单独生产各种型号帐篷的数量如图所示:

根据以上信息,下列判断错误的是( )
A. 其中的D型帐篷占帐篷总数的10%
B. 单独生产B型帐篷的天数是单独生产C型帐篷天数的3倍
C. 单独生产A型帐篷与单独生产D型帐篷的天数相等
D. 单独生产B型帐篷的天数是单独生产A型帐篷天数的2倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图1至图3中,点B是线段AC的中点,点D是线段CE的中点。四边形BCGF和CDHN都是正方形。AE的中点是M,FH的中点是P。
(1)如图1,点A、C、E在同一条直线上,根据图形填空:
①△BMF是__________三角形;
②MP与FH的位置关系是___________;MP与FH的数量关系是____________;
(2)将图1中的CE绕点C顺时针旋转一个锐角,得到图2,解答下列问题:
①证明:△BMF是等腰三角形;
②(1)中得到的MP与FH的位置关系和数量关系是否仍然成立?证明你的结论;
(3)将图2中的CE缩短到图3的情况,(2)中的三个结论还成立吗?(成立的不需要说明理由,不成立的需要说明理由)



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com