
分析 x2-5可以利用平方差公式即可分解;
后边的三个式子分解可以令每个式子等于0,解方程,则可以直接写出分解以后的结果.
解答 解:x2-5=(x+$\sqrt{5}$)(x-$\sqrt{5}$);
解x2+x-1=0得x=$\frac{-1±\sqrt{5}}{2}$,则x2+x-1=(x+$\frac{-1+\sqrt{5}}{2}$)(x-$\frac{-1-\sqrt{5}}{2}$);
解x2-2x-1=0得x=1±$\sqrt{2}$,则x2-2x-1=(x+1-$\sqrt{2}$)(x-1+$\sqrt{2}$);
解3x2-x-1=0得x=$\frac{1±\sqrt{13}}{6}$,则3x2-x-1=3(x+$\frac{1+\sqrt{13}}{6}$)(x-$\frac{1+\sqrt{13}}{6}$).
故答案是:(x+$\sqrt{5}$)(x-$\sqrt{5}$);(x+$\frac{-1+\sqrt{5}}{2}$)(x-$\frac{-1-\sqrt{5}}{2}$);(x+1-$\sqrt{2}$)(x-1+$\sqrt{2}$);3(x+$\frac{1+\sqrt{13}}{6}$)(x-$\frac{1+\sqrt{13}}{6}$).
点评 本题考查实数范围内的因式分解,因式分解的步骤为:一提公因式;二看公式,如果是关于每个字母的二次三项式,可以解对应的方程求得方程的解,然后写出分解的结果,在实数范围内进行因式分解的式子的结果一般要分到出现无理数为止


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:
如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
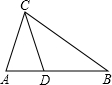 如图,下列四个条件:
如图,下列四个条件:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com