
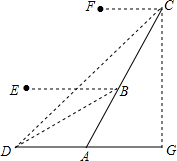
 某景区为了更好地吸引游客,开发了乘热气球游览的项目,如图,一名游客在A点乘坐热气球沿倾斜角为60°的方向上升,到达B点时测得点D的俯角为30°,到达C点时测得点D的俯角为45°,已知AB=500米,求点C到地面的距离.(参考数据:$\sqrt{3}$≈1.732)
某景区为了更好地吸引游客,开发了乘热气球游览的项目,如图,一名游客在A点乘坐热气球沿倾斜角为60°的方向上升,到达B点时测得点D的俯角为30°,到达C点时测得点D的俯角为45°,已知AB=500米,求点C到地面的距离.(参考数据:$\sqrt{3}$≈1.732) 分析 如图作BM⊥DG于M.在RT△ABM中求出BM,在RT△DBM中求出DB,再证明∠BDC=∠BCD=15°,得到BD=BC,最后在RT△ACG中求出CG即可.
解答 解: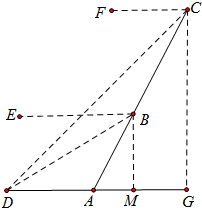 如图作BM⊥DG于M.在RT△ABM中,∵∠BMA=90°,AB=500,∠BAM=60°,
如图作BM⊥DG于M.在RT△ABM中,∵∠BMA=90°,AB=500,∠BAM=60°,
∴AM=250,BM=250$\sqrt{3}$,
在RT△DBM中,∵BM=250$\sqrt{3}$,∠BDM=30°,
∴DB=2BM=500$\sqrt{3}$,
∵∠CDG=∠DCG=45°,∠BDM=∠ACG=30°,
∴∠BDC=∠BCD=15°,
∴BD=BC=500$\sqrt{3}$,
∴AC=500+500$\sqrt{3}$,
在RT△ACG中,∵∠G=90°,AC=500+500$\sqrt{3}$,∠ACG=30°,
∴AG=$\frac{1}{2}$AC=250+250$\sqrt{3}$,CG=$\sqrt{3}$AG=250$\sqrt{3}$+750≈1183m
∴点C到地面的距离为1183m.
点评 本题考查解直角三角形、俯角、仰角、特殊角三角函数等知识,解题的关键是直角三角形中只要已知一角一边即可解直角三角形,属于中考常考题型.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:选择题
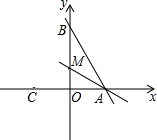 如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )| A. | (0,4) | B. | (0,3) | C. | (-4,0) | D. | (0,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com