
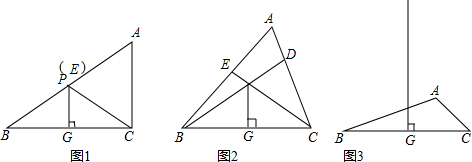
分析 (1)由PG是BC的垂直平分线可得出“PB=PC,∠PBC=∠PCB”,通过角的计算可以得出∠APC=∠PAC,结合等腰三角形的性质即可得出CP=CA,通过等量变换即可得出结论;
(2)过点B作BF⊥CE于点F,过点C作CM⊥BD于点M,结合全等三角形的判定定理得出△PBF≌△PCM,从而得出BF=CM;再通过边角关系找出∠BEF=∠CDM,即在△BEF和△CMD中满足全等三角形的判定定理(AAS)证出△BEF≌△CMD,结合全等三角形的性质即可得出结论;
(3)过点B作BF⊥PC于点F,过点C作CM⊥PB于点M,证明方法等同于(2).
解答 (1)BE=CD.
证明:∵PG⊥BC,G为BC的中点,
∴PB=PC,∠PBC=∠PCB.
∵∠APC=∠PBC+∠PCB=2∠PBC,∠BAC=2∠PBC,
∴∠APC=∠PAC,
∴CP=CA,
∴BP=CA.
∵E与P重合,D与A重合,
∴BE=CD.
故答案为:BE=CD.
(2)BE=CD.
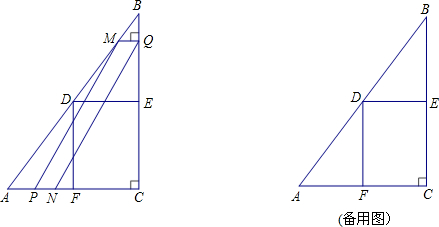
证明:过点B作BF⊥CE于点F,过点C作CM⊥BD于点M,如图(一)所示.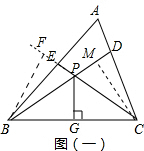
∵BF⊥CE,CM⊥BD,
∴∠PFB=∠PMC=90°.
∵PG是BC的垂直平分线,
∴PB=PC.
在△PBF和△PCM中,
$\left\{\begin{array}{l}{∠PFB=∠PMC}\\{∠BPF=∠CPM}\\{PB=PC}\end{array}\right.$,
∴△PBF≌△PCM(AAS),
∴BF=CM.
∵PB=PC,
∴∠BPE=∠PBC+∠PCB=2∠PBC.
∵∠A=2∠PBC,
∴∠A=∠BPE.
∠EPD+∠BPE=∠EPD+∠A=180°,
∠AEP+∠ADP=180°.
又∠AEP=∠BEF,∠ADP+∠CDM=180°,
∴∠BEF=∠CDM.
在△BEF和△CMD中,
$\left\{\begin{array}{l}{∠BEF=∠CDM}\\{∠BFE=CMD=90°}\\{BF=CM}\end{array}\right.$,
∴△BEF≌△CMD(AAS),
∴BE=CD.
(3)BE=CD.
证明:过点B作BF⊥PC于点F,过点C作CM⊥PB于点M,如图(二)所示.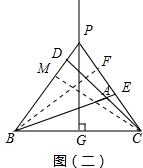
∵BF⊥PC,CM⊥PB,
∴∠PFB=∠PMC=90°.
∵PG是BC的垂直平分线,
∴PB=PC.
在△PBF和△PCM中,
$\left\{\begin{array}{l}{∠PFB=∠PMC}\\{∠BPF=∠CPM}\\{PB=PC}\end{array}\right.$,
∴△PBF≌△PCM(AAS),
∴BF=CM.
∵PB=PC,
∴∠PBC=∠PCB,
∵∠DAE=∠BAC=2∠PBC,∠P+∠PBC+∠PCB=180°,
∴∠DAE+∠P=180°,
∴∠AEP+∠PDA=180°.
又∵∠PDA+∠MDC=180°,
∴∠AEP=∠MDC,即∠BEF=∠CDM.
在△BEF和△CMD中,
$\left\{\begin{array}{l}{∠BEF=∠CDM}\\{∠BFE=CMD=90°}\\{BF=CM}\end{array}\right.$,
∴△BEF≌△CMD(AAS),
∴BE=CD.
点评 本题考查了垂直平分线的性质、等腰三角形的性质、全等三角形的判定及性质以及角的计算,解题的关键:(1)利用等腰三角形的性质找出BP=CA;(2)证出△BEF≌△CMD;(3)证出△BEF≌△CMD.本题属于中档题,难度不大,解决该题型题目时,通过角的计算找出相等的角,再根据全等三角形的判定定理证明三角形全等是关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
 某景区为了更好地吸引游客,开发了乘热气球游览的项目,如图,一名游客在A点乘坐热气球沿倾斜角为60°的方向上升,到达B点时测得点D的俯角为30°,到达C点时测得点D的俯角为45°,已知AB=500米,求点C到地面的距离.(参考数据:$\sqrt{3}$≈1.732)
某景区为了更好地吸引游客,开发了乘热气球游览的项目,如图,一名游客在A点乘坐热气球沿倾斜角为60°的方向上升,到达B点时测得点D的俯角为30°,到达C点时测得点D的俯角为45°,已知AB=500米,求点C到地面的距离.(参考数据:$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
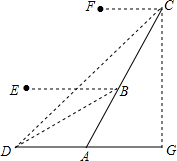
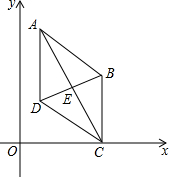 如图,在平面直角坐标系中,点A(1,4)B(m,n)(m>2),D(1,q)(q<n),点B、D在直线y=$\frac{1}{2}$x+1上,四边形ABCD的对角线AC,BD相交于点E.且AB∥CD,点C在x轴上,BE=DE.求证:四边形ABCD是菱形.
如图,在平面直角坐标系中,点A(1,4)B(m,n)(m>2),D(1,q)(q<n),点B、D在直线y=$\frac{1}{2}$x+1上,四边形ABCD的对角线AC,BD相交于点E.且AB∥CD,点C在x轴上,BE=DE.求证:四边形ABCD是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com