
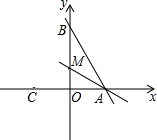
 如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )| A. | (0,4) | B. | (0,3) | C. | (-4,0) | D. | (0,-3) |
分析 首先求出直线与坐标轴交点坐标,进而得出BO,AO的长,再利用勾股定理求出AB的长;根据翻折变换的性质得出MB=MC,AB=AC=10,然后根据勾股定理直接求出MO的长,即可得出答案.
解答 解:∵直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,
∴y=0时,x=6,则A点坐标为:(6,0),
x=0时,y=8,则B点坐标为:(0,8);
∴BO=8,AO=6,
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10, 直线AB沿AM折叠,点B恰好落在x轴上的点C处,
直线AB沿AM折叠,点B恰好落在x轴上的点C处,
∴AB=AC=10,MB=MC,
∴OC=AC-OA=10-6=4.
设MO=x,则MB=MC=8-x,
在Rt△OMC中,OM2+OC2=CM2,
∴x2+42=(8-x)2,
解得:x=3,
故M点坐标为:(0,3).
故选B.
点评 此题主要考查了翻折变换的性质以及勾股定理的应用和一次函数图象与几何变换等知识,根据已知得出A,B两点坐标以及利用翻折变换的性质得出MB=MC,AB=AC是解题关键.


科目:初中数学 来源: 题型:选择题
 某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况.如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为( )
某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况.如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为( )| A. | 300米 | B. | 150$\sqrt{2}$米 | C. | 900米 | D. | (300$\sqrt{3}$+300)米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
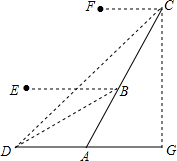 某景区为了更好地吸引游客,开发了乘热气球游览的项目,如图,一名游客在A点乘坐热气球沿倾斜角为60°的方向上升,到达B点时测得点D的俯角为30°,到达C点时测得点D的俯角为45°,已知AB=500米,求点C到地面的距离.(参考数据:$\sqrt{3}$≈1.732)
某景区为了更好地吸引游客,开发了乘热气球游览的项目,如图,一名游客在A点乘坐热气球沿倾斜角为60°的方向上升,到达B点时测得点D的俯角为30°,到达C点时测得点D的俯角为45°,已知AB=500米,求点C到地面的距离.(参考数据:$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com