
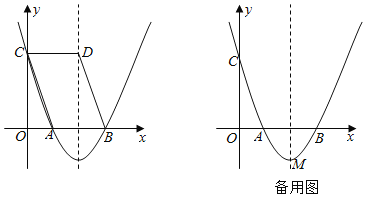
【题目】如图,已知二次函数y=ax2﹣8ax+6(a>0)的图象与x轴分别交于A、B两点,与y轴交于点C,点D在抛物线的对称轴上,且四边形ABDC为平行四边形.
(1)求此抛物线的对称轴,并确定此二次函数的表达式;
(2)点E为x轴下方抛物线上一点,若△ODE的面积为12,求点E的坐标;
(3)在(2)的条件下,设抛物线的顶点为M,点P是抛物线的对称轴上一动点,连接PE、EM,过点P作PE的垂线交抛物线于点Q,当∠PQE=∠EMP时,求点Q到抛物线的对称轴的距离.
【答案】(1)x=4,y=![]() x2﹣4x+6;(2)(3,-
x2﹣4x+6;(2)(3,-![]() );(3)4或2+
);(3)4或2+![]()
【解析】
(1)先求出对称轴为x=4,进而求出AB=4,进而求出点A,B坐标,即可得出结论;
(2)根据E点在抛物线y=![]() x2﹣4x+6上,设E(m,
x2﹣4x+6上,设E(m,![]() m2﹣4m+6),作EN⊥y轴于N,利用面积的和差:S梯形CDEN﹣S△OCD﹣S△OEN=S△ODE建立方程求解,即可得出结论;
m2﹣4m+6),作EN⊥y轴于N,利用面积的和差:S梯形CDEN﹣S△OCD﹣S△OEN=S△ODE建立方程求解,即可得出结论;
(3)①当点Q在对称轴右侧时,先判断出点E,M,Q,P四点共圆,得出∠EMQ=90°,利用同角的余角相等判断出∠EMF=∠HGM,得出tan∠EMF=![]() =2,得出HG=
=2,得出HG=![]() HM=1,进而求出Q(8,6),得出结论;
HM=1,进而求出Q(8,6),得出结论;
②当点Q在对称轴左侧时,先判断出△PDQ∽△EFP,得出![]() ,进而判断出DP=
,进而判断出DP=![]() ,PF=2QD,即可得出结论.
,PF=2QD,即可得出结论.
解:(1)对称轴为直线x=﹣![]() ,则CD=4,
,则CD=4,
∵四边形ABDC为平行四边形,
∴DC∥AB,DC=AB,
∴DC=AB=4,
∴A(2,0),B(6,0),
把点 A(2,0)代入得y=ax2﹣8ax+12得4a﹣16a+6=0,解得a=![]() ,
,
∴二次函数解析式为y=![]() x2﹣4x+6;
x2﹣4x+6;
(2)如图1,设E(m,![]() m2﹣4m+6),其中2<m<6,作EN⊥y轴于N,
m2﹣4m+6),其中2<m<6,作EN⊥y轴于N,
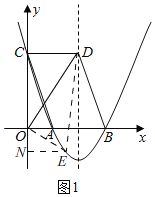
∵S梯形CDEN﹣S△OCD﹣S△OEN=S△ODE,
∴![]() (4+m)(6﹣
(4+m)(6﹣![]() m2+4m﹣6)﹣
m2+4m﹣6)﹣![]() ×4×6﹣
×4×6﹣![]() m(﹣
m(﹣![]() m2+4m﹣6)=12,
m2+4m﹣6)=12,
化简得:m2﹣11m+24=0,解得m1=3,m2=8(舍),
∴点E的坐标为(3,﹣![]() );
);
(3)①当点Q在对称轴右侧时,如图2,
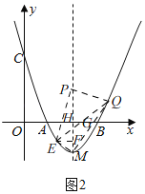
过点E作EF⊥PM于F,MQ交x轴于G,
∵∠PQE=∠PME,
∴点E,M,Q,P四点共圆,
∵PE⊥PQ,
∴∠EPQ=90°,
∴∠EMQ=90°,
∴∠EMF+∠HMG=90°,
∵∠HMG+∠HGM=90°,
∴∠EMF=∠HGM,
在Rt△EFM中,EF=1,FM=![]() ,tan∠EMF=
,tan∠EMF=![]() =2,
=2,
∴tan∠HGM=2,
∴![]() ,
,
∴HG=![]() HM=1,
HM=1,
∴点G(5,0),
∵M(4,﹣2),
∴直线MG的解析式为y=2x﹣10①,
∵二次函数解析式为y=![]() x2﹣4x+6②,
x2﹣4x+6②,
联立①②解得,![]() (舍)或
(舍)或![]() ,
,
∴Q(8,6),
∴点Q到对称轴的距离为8﹣4=4;
②当点Q在对称轴左侧时,如图3,
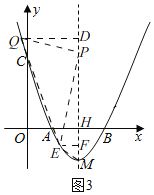
过点E作EF⊥PM于F,过点Q作QD⊥PM于D,
∴∠DQP+∠QPD=90°,
∵∠EPQ=90°,
∴∠DPQ+∠FPE=90°,
∴∠DQP=∠FPE,
∵∠PDQ=∠EFP,
∴△PDQ∽△EFP,
∴![]() ,
,
由①知,tan∠PQE=![]() =2,
=2,
∵EF=1,
∴![]() =
=![]() ,
,
∴DP=![]() ,PF=2QD,
,PF=2QD,
设Q(n,![]() n2﹣4n+6),
n2﹣4n+6),
∴DQ=4﹣n,DH=![]() n2﹣4n+6,
n2﹣4n+6,
∴PF=DH+FH﹣DP=![]() n2﹣4n+6+
n2﹣4n+6+![]() ﹣
﹣![]() =
=![]() n2﹣4n+7,
n2﹣4n+7,
∴![]() n2﹣4n+7=2(4﹣n),
n2﹣4n+7=2(4﹣n),
∴n=2+![]() (舍)或n=2﹣
(舍)或n=2﹣![]() ,
,
∴DQ=4﹣n=2+![]() ,
,
即点Q到对称轴的距离为4或2+![]() .
.


科目:初中数学 来源: 题型:
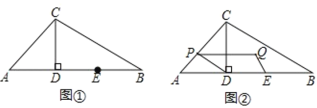
【题目】如图①,在△ABC 中,CD⊥AB 于点 D,AD=CD=2,BD=4,点 E 是线段BD 的中点,点 P 从点 A 出发,沿折线 AC-CB 向终点 B 运动,点 P 在边 AC 上的速度为每秒![]() 个单位长度,P在BC边上的速度为
个单位长度,P在BC边上的速度为![]() 个单位长度,设P的运动时间为 t(秒).
个单位长度,设P的运动时间为 t(秒).
(1)用含 t 的代数式表示点 P 到直线 AB 的距离.
(2)如图②,作点 P 关于直线 CD 的对称点 Q,设以 D、E、Q、P 为顶点的四边形的面积为 S(平方单位),求 S 与 t 之间的函数关系式.
(3)当点 P 在边 BC 上时,在△BCD 的边上(不包括顶点)存在点 H,使四边形 DEPH为轴对称图形,直接写出此时线段 CP 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数![]() (k≠0)的图象过点C,则该反比例函数的表达式为( )
(k≠0)的图象过点C,则该反比例函数的表达式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
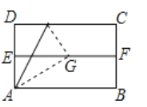
【题目】如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平,再一次折叠,使点D落到EF上点G处,并使折痕经过点A,已知BC=2,则线段EG的长度为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中抽取一张,将该卡片上的数字记为
的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中抽取一张,将该卡片上的数字记为![]() ;不放回,再从中抽取一张,将该卡片上的数字记为
;不放回,再从中抽取一张,将该卡片上的数字记为![]() ,则使关于
,则使关于![]() 的不等式组
的不等式组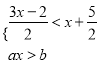 的解集中有且只有
的解集中有且只有![]() 个非负整数解的概率为 .
个非负整数解的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五名学生投篮球,每人投10次,统计他们每人投中的次数.得到五个数据,并对数据进行整理和分析给出如下信息:
平均数 | 中位数 | 众数 |
m | 6 | 7 |
则下列选项正确的是( )
A.可能会有学生投中了8次
B.五个数据之和的最大值可能为30
C.五个数据之和的最小值可能为20
D.平均数m一定满足![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点D是
,点D是![]() 外一点,点D与点C在直线
外一点,点D与点C在直线![]() 的异侧,且点
的异侧,且点![]() 不共线,连接
不共线,连接![]() .
.


(1)如图1,当![]() 时,画出图形,直接写出
时,画出图形,直接写出![]() 之间的数量关系;
之间的数量关系;
(2)当![]() 时,利用图2,继续探究
时,利用图2,继续探究![]() 之间的数量关系并证明;
之间的数量关系并证明;
(提示:尝试运用图形变换,将要研究的有关线段尽可能转移到一个三角形中)
(3)当![]() 时,进一步探究
时,进一步探究![]() 之间的数量关系,并用含
之间的数量关系,并用含![]() 的等式直接表示出它们之间的关系.
的等式直接表示出它们之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(2)求抛物线与![]() 轴的交点坐标;
轴的交点坐标;
(3)已知点![]() ,
,![]() ,如果抛物线与线段
,如果抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com