
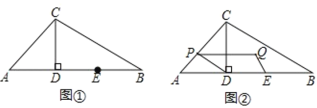
【题目】如图①,在△ABC 中,CD⊥AB 于点 D,AD=CD=2,BD=4,点 E 是线段BD 的中点,点 P 从点 A 出发,沿折线 AC-CB 向终点 B 运动,点 P 在边 AC 上的速度为每秒![]() 个单位长度,P在BC边上的速度为
个单位长度,P在BC边上的速度为![]() 个单位长度,设P的运动时间为 t(秒).
个单位长度,设P的运动时间为 t(秒).
(1)用含 t 的代数式表示点 P 到直线 AB 的距离.
(2)如图②,作点 P 关于直线 CD 的对称点 Q,设以 D、E、Q、P 为顶点的四边形的面积为 S(平方单位),求 S 与 t 之间的函数关系式.
(3)当点 P 在边 BC 上时,在△BCD 的边上(不包括顶点)存在点 H,使四边形 DEPH为轴对称图形,直接写出此时线段 CP 的长.
【答案】(1)![]() 或
或![]() ;(2)
;(2)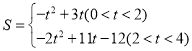 ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)分两种情况:
①当P在边AC上时,如图1,根据△APG是等腰直角三角形,可得![]() ;
;
②当P在边BC上时,如图2,根据三角函数sin∠B,可得PG的长;
(2)分两种情况:
①当0<t<2时,P在边AC上,如图3,②当2<t<4时,P在边BC上,如图4,
四边形PQDE是梯形,根据梯形面积公式代入可得结论;
(3)分4种情况:
①如图5,当四边形DEPH是矩形时;②如图6,当四边形DEPH是等腰梯形时;③如图7,过D作DP⊥BC于P,过E作EH⊥PD,交CD于H,④如图8,过E作EP⊥BC于P,在BC上取点H,使PH=EP,连接DH,③和④是筝形;分别求出各情况的CP的长即可.
(1)过P作PG⊥AB于G,
分两种情况:
①当P在边AC上时,如图1,
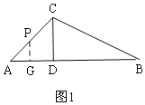
Rt△ADC中,AD=CD=2,
∴∠A=45°,
∴△APG是等腰直角三角形,
由勾股定理得:AC=![]() ,
,
P走完AC段所花时间为:![]() (秒),
(秒),
P在边AC上,即0![]() 2时,
2时,
由题意得:AP=![]() ,
,
∴AG=PG= AP![]() =
=![]() ,
,
即点P到直线AB的距离是t;
②当P在边BC上时,如图2,
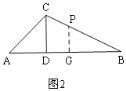
BC=![]() ,
,
P走完BC段所花时间为:![]() ,
,
P在边BC上,即2![]() 4时,
4时,
由题意得:CP=![]() ,
,
∴BP= BC - CP =![]() ,
,
sin∠B=![]() ,
,
∴![]() ,
,
∴PG=![]() ,
,
即点P到直线AB的距离是![]() ;
;
(2)分两种情况:
①当0<t<2时,P在边AC上,如图3,
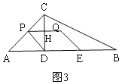
设PQ与CD交于H,
∵点P关于直线CD的对称点Q,
∴PQ⊥CD,
∵AB⊥CD,
∴PQ∥AB,
∴△CPH∽△CAD,
∴![]() ,
,
∴![]() ,
,
∴PH=CH=![]() ,PQ=2PH=
,PQ=2PH=![]() ,
,
∵BD=4,点 E 是线段BD 的中点,
∴DE=![]() ,
,
∴DH=CD-CH ![]() ,
,
∴![]() ;
;
②当2<t<4时,P在边BC上,如图4,
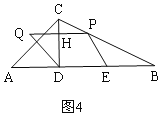
设PQ与CD交于H,
由题意得:CP![]() ,
,
同理PQ∥AB,
∴△CPH∽△CBD,
∴![]() ,
,
∴![]() ,
,
∴PH=2(![]() ),CH=
),CH=![]() ,
,
∴DH=CD-CH=2![]() (
(![]() )=
)=![]() ,PQ=2PH=4
,PQ=2PH=4![]() )=
)=![]() ,
,
∴![]() ;
;
(3)分4种情况:
①如图5,
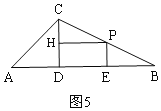
当四边形DEPH是矩形时,四边形DEPH是轴对称图形,
∴PE∥CD,
∵点 E 是线段BD 的中点,
∴P是BC的中点,
∴CP=![]() ;
;
②如图6,
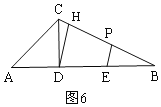
当四边形DEPH是等腰梯形时,四边形DEPH是轴对称图形,
∴DH∥PE,
则BD=BH=4,BE=PB=2,
此时CP![]() ;
;
③如图7,
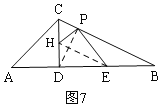
过D作DP⊥BC于P,过E作EH⊥PD,交CD于H,
∴EH∥BC,
∵E是BD的中点,
∴EH是PD的中垂线,
∴PH=DH,PE=DE,
∴四边形DEPH为轴对称图形,![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
由勾股定理得:CP=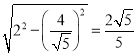 ;
;
④如图8,
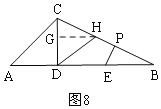
过E作EP⊥BC于P,在BC上取点H,使PH=EP,连接DH,过H作HG⊥CD于G,
∵Rt△EPB![]() Rt△CDB中,BE=2,
Rt△CDB中,BE=2,
∴![]() ,
,
∴![]() ,
,
∴EP=![]() ,PB=
,PB=![]() ,
,
CH=BC-PH-PB=![]() ,
,
∵GH∥BD,
∴△CGH∽△CDB,
∴![]() ,
,
∴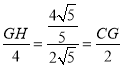 ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
由勾股定理得: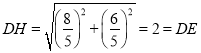 ,
,
∴四边形DEPH为轴对称图形,
此时CP=CH+HP=![]() ;
;
综上所述,CP的长为:![]() 或
或![]() 或
或![]() 或
或![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 内接于⊙
内接于⊙![]() ,直径
,直径![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .过点
.过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .
.
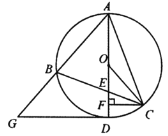
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
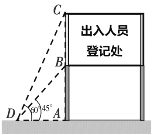
【题目】2020春节期间,为了进一步做好新型冠状病毒感染的肺炎疫情防控工作,防止新型肺炎外传,切断传播途径.项城市市区各入口一些主要路段均设立了检测点,对出入人员进行登记和体温检测。下图为一关口的警示牌,已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求警示牌BC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如图所示的函数图象是由函数y=(x﹣1)2+1(x≥0)的图象C1和图象C2组成中心对称图形,对称中心为点(0,2).已知不重合的两点A、B分别在图象C1和C2上,点A、B的横坐标分别为a、b,且a+b=0.当b<x≤a时该函数的最大值和最小值均与a、b的值无关,则a的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 均是
均是![]() 的函数,下表是
的函数,下表是![]() 与
与![]() 的几组对应值.
的几组对应值.

小聪根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,分别对函数
之间的变化规律,分别对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小聪的探究过程,请补充完整:
(1)如图,在同一平面直角坐标系![]() 中,描出上表中各组数值所对应的点
中,描出上表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 的图象;
的图象;

(2)结合画出的函数图象,解决问题:
①当![]() 时,对应的函数值
时,对应的函数值![]() 约为_________;
约为_________;
②写出函数![]() 的一条性质:_________________________;
的一条性质:_________________________;
③当![]() 时,
时,![]() 的取值范围是_________________________.
的取值范围是_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
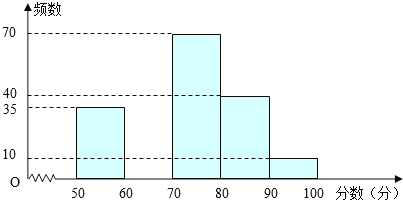
根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个三角形一条边上的高与这条边的比值是![]() ,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.
,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.
(1)如图,在△ABC中,AC=8,BC=5,![]() ,试判断△ABC是否是“准黄金”三角形,请说明理由.
,试判断△ABC是否是“准黄金”三角形,请说明理由.
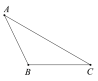
(2)如图,△ABC是“准黄金”三角形,BC是“金底”,把△ABC沿BC翻折得到△DBC,AD交BC的延长线于点E,若点C恰好是△ABD的重心,求![]() 的值.
的值.
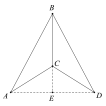
(3)如图,![]() ,且直线
,且直线![]() 与
与![]() 之间的距离为4,“准黄金”△ABC的“金底”BC在直线
之间的距离为4,“准黄金”△ABC的“金底”BC在直线![]() 上,点A在直线
上,点A在直线![]() 上,
上,![]() =
=![]() ,若∠ABC是钝角,将△ABC绕点C按顺时针方向旋转得到△
,若∠ABC是钝角,将△ABC绕点C按顺时针方向旋转得到△![]() ,线段
,线段![]() 交
交![]() 于点D.当点
于点D.当点![]() 落在直线
落在直线![]() 上时,则
上时,则![]() 的值为____.
的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
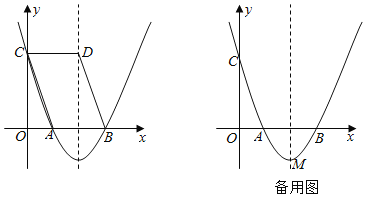
【题目】如图,已知二次函数y=ax2﹣8ax+6(a>0)的图象与x轴分别交于A、B两点,与y轴交于点C,点D在抛物线的对称轴上,且四边形ABDC为平行四边形.
(1)求此抛物线的对称轴,并确定此二次函数的表达式;
(2)点E为x轴下方抛物线上一点,若△ODE的面积为12,求点E的坐标;
(3)在(2)的条件下,设抛物线的顶点为M,点P是抛物线的对称轴上一动点,连接PE、EM,过点P作PE的垂线交抛物线于点Q,当∠PQE=∠EMP时,求点Q到抛物线的对称轴的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com