Question

【题目】如图，在四边形ABCD中，AD=AB=BC，连接AC，且∠ACD=30°，tan∠BAC=，CD=3，则AC= .

Answer 1

【答案】或
【解析】解：过点D、B分别作DE⊥AC，BH⊥AC，垂足分别为E、H，设AC=x．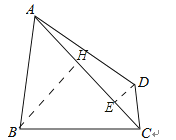

在Rt△CDE中，DC=3，∠DCE=30°，
∴，．
∴DE=，CE=．
则AE=x﹣，
在Rt△AED中，由勾股定理得：AD2=AE2+DE2=，
∵AB=BC，BH⊥AC，
∴AH=AC=x，
∵tan∠BAC=，
∴BH=AH=x
在Rt△ABH中，由勾股定理得：AB2=BH2+AH2 ，
∴．
∵AB=AD，
∴
解得：x1=6，x2=．
∴AC=6或．
过点D、B分别作DE⊥AC，BH⊥AC，垂足分别为E、H，设AC=x，先求得AE（用含x的式子表示）和DE的长，根据勾股定理可表示出AD2 ， 然后根据等腰三角形三线合一的性质可知：AH=x，然后根据锐角三角函数的定义可求得HB（用含x的式子表示）的长，根据勾股定理可表示出AB2 ， 然后根据AB=AD，列方程求解即可．