
【题目】某校八年级甲.乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图:
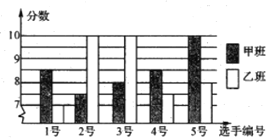
(1)根据上图求出下表所缺数据:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8 | 1.6 |
(2)根据上表中的平均数、中位数和方差你认为哪班的成绩较好?并说明你的理由.
【答案】(1)甲:8.5,0.7;乙:8.5,10;(2)甲班的成绩更稳定,理由见解析.
【解析】
(1)根据众数、方差和平均数的定义及公式分别进行解答即可;
(2)从平均数、中位数以及方差的意义三个方面分别进行解答即可得出答案.
(1)甲班的众数是8.5;
方差是:![]() ×[(8.5-8.5)2+(7.5-8.5)2+(8-8.5)2+(8.5-8.5)2+(10-8.5)2]=0.7.
×[(8.5-8.5)2+(7.5-8.5)2+(8-8.5)2+(8.5-8.5)2+(10-8.5)2]=0.7.
乙班的平均数是:![]() (7+10+10+7.5+8)=8.5,
(7+10+10+7.5+8)=8.5,
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | 8.5 | 0.7 |
乙班 | 8.5 | 8 | 10 | 1.6 |
故答案为:8.5,0.7;8.5;
(2)因为甲、乙两班成绩的平均数相同,而甲班成绩的中位数高于乙班的中位数,甲班的方差小于乙班的方差,
所以甲班的成绩较好.


科目:初中数学 来源: 题型:
【题目】如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
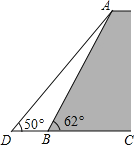
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮要利用废纸板做一个三棱柱形状的无盖的笔筒,设计三棱柱的立体模型如图所示.
(1)请画出该立体模型的三视图;
(2)该笔筒至少要用多少废纸板?
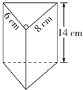
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),点
的左侧),点![]() 的坐标为
的坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() .动点
.动点![]() 在
在![]() 轴上运动,过点
轴上运动,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
(Ⅰ)求抛物线的解析式和直线![]() 的解析式;
的解析式;
(Ⅱ)当点![]() 在线段
在线段![]() 上运动时,求线段
上运动时,求线段![]() 的最大值;
的最大值;
(Ⅲ)当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,直接写出
为顶点的四边形是平行四边形时,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN.
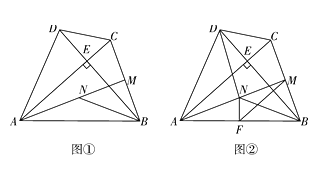
(1)求证:BN平分∠ABE;
(2)若BD=1,连结DN,当四边形DNBC为平行四边形时,求线段BC的长;
(3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
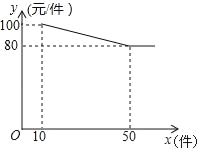
【题目】服装厂批发某种服装,每件成本为65元,规定不低于10件可以批发,其批发价y(元/件)与批发数量x(件)(x为正整数)之间所满足的函数关系如图所示.
(1)求y与x之间所满足的函数关系式,并写出x的取值范围;
(2)设服装厂所获利润为w(元),若10≤x≤50(x为正整数),求批发该种服装多少件时,服装厂获得利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且 ![]() .下列结论: ①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论: ①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④CD2=CECA.其中正确的结论是________(把你认为正确结论的序号都填上)
;④CD2=CECA.其中正确的结论是________(把你认为正确结论的序号都填上)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com