
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= ![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤ ![]() 的解集.
的解集.
【答案】
(1)
解:∵OB=2OA=3OD=6,
∴OB=6,OA=3,OD=2,
∵CD⊥OA,
∴DC∥OB,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CD=10,
∴点C坐标(﹣2,10),B(0,6),A(3,0),
∴ ![]() 解得
解得 ![]() ,
,
∴一次函数为y=﹣2x+6.
∵反比例函数y= ![]() 经过点C(﹣2,10),
经过点C(﹣2,10),
∴n=﹣20,
∴反比例函数解析式为y=﹣ ![]()
(2)
解:由 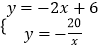 解得
解得 ![]() 或
或 ![]() ,
,
故另一个交点坐标为(5,﹣4)
(3)
解:由图象可知kx+b≤ ![]() 的解集:﹣2≤x<0或x≥5.
的解集:﹣2≤x<0或x≥5.
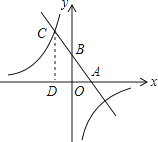
【解析】(1)先求出A、B、C坐标,再利用待定系数法确定函数解析式.(2)两个函数的解析式作为方程组,解方程组即可解决问题.(3)根据图象一次函数的图象在反比例函数图象的下方,即可解决问题,注意等号.本题考查一次函数与反比例函数的交点问题,解题的关键是学会利用待定系数法确定函数解析式,知道两个函数图象的交点坐标可以利用解方程组解决,学会利用图象确定自变量取值范围,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )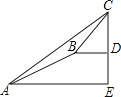
A.8.1米
B.17.2米
C.19.7米
D.25.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x+2与双曲线相交于点A(m,3),与x轴交于点C.
x+2与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张.
(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A,B,C,D表示);
(2)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 40 | 60 | 100 |
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E,F的人数分别为80,70
D.喜欢选修课C的人数最少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d= ![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y= ![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,射线CM⊥BC,且BC=4,AB=1,点P是线段BC(不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

(1)如图1,若BP=3,求△ABP的周长;
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并说明理由;
(3)若△PDC是等腰三角形,作点B关于AP的对称点B′,连结B′D,则B′D=_____.(请直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com