
如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A.1,2,3 B.1,1,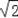
 C.1,1,
C.1,1,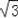
 D.1,2,
D.1,2,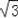

D【考点】解直角三角形.
【专题】新定义.
【分析】A、根据三角形三边关系可知,不能构成三角形,依此即可作出判定;
B、根据勾股定理的逆定理可知是等腰直角三角形,依此即可作出判定;
C、解直角三角形可知是顶角120°,底角30°的等腰三角形,依此即可作出判定;
D、解直角三角形可知是三个角分别是90°,60°,30°的直角三角形,依此即可作出判定.
【解答】解:A、∵1+2=3,不能构成三角形,故选项错误;
B、∵12+12=(
 )2,是等腰直角三角形,故选项错误;
)2,是等腰直角三角形,故选项错误;
C、底边上的高是
 =
=
 ,可知是顶角120°,底角30°的等腰三角形,故选项错误;
,可知是顶角120°,底角30°的等腰三角形,故选项错误;
D、解直角三角形可知是三个角分别是90°,60°,30°的直角三角形,其中90°÷30°=3,符合“智慧三角形”的定义,故选项正确.
故选:D.
【点评】考查了解直角三角形,涉及三角形三边关系,勾股定理的逆定理,等腰直角三角形的判定,“智慧三角形”的概念.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
问题提出
 我们在分析解决某
我们在分析解决某 些数学问题时,经常要比较两个数或代数式的大小,而“作差法”就是常用的解决问题的策略之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小.
些数学问题时,经常要比较两个数或代数式的大小,而“作差法”就是常用的解决问题的策略之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小.
(1) 利用“作差法” 解决问题
如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是
a、b的小正方形及两个 矩形,设两个小正方形面积之和为M,两个
矩形,设两个小正方形面积之和为M,两个
矩形面积之和为N,试比较M与N的大小.
(2)类比应用
 ①已知甲、乙两人的速度分别是
①已知甲、乙两人的速度分别是 =
= 千米/小时、
千米/小时、
 千米/小时(
千米/小时(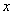 、
、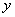 是正数,且
是正数,且 ),试比较
),试比较 的大小.
的大小.
②如图2,在边长为a的正方形ABCD中,以A为圆心, 为
为
半径画弧交AB、AD于点E、F,以CD为直径画弧,若图中阴影部分
的面积分别为S1,S2,试比较S1与S2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
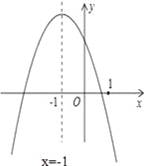
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列五条结论:
①abc<0;②4ac﹣b2<0;③4a+c<2b;④3b+2c<0;⑤m(am+b)+b<a(m≠﹣1)
其中正确的结论是 (把所有正确的结论的序号都填写在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,C,P是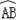
 上两点,AB=13,AC=5.
上两点,AB=13,AC=5.
(1)如图(1),若点P是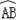
 的中点,求PA的长;
的中点,求PA的长;
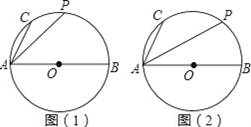
(2)如图(2),若点P是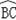
 的中点,求PA的长.
的中点,求PA的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com