
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列五条结论:
①abc<0;②4ac﹣b2<0;③4a+c<2b;④3b+2c<0;⑤m(am+b)+b<a(m≠﹣1)
其中正确的结论是 (把所有正确的结论的序号都填写在横线上)
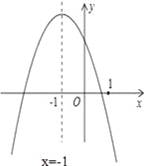

②④⑤
【考点】二次函数图象与系数的关系.
【专题】二次函数图象及其性质;二次函数的应用.
【分析】根据抛物线开口方向、对称轴、与y轴交点可判断①;根据抛物线与x轴交点个数可判断②;根据x=0与x=﹣2关于对称轴x=﹣1对称,且x=0时y>0,可判断③;根据x=1时,y<0,且对称轴为x=﹣1可判断④;由抛物线在x=﹣1时有最大值,可判断⑤.
【解答】解:①由抛物线图象得:开口向下,即a<0;c>0,﹣
 =﹣1<0,即b=2a<0,
=﹣1<0,即b=2a<0,
∴abc>0,选项①错误;
②∵抛物线图象与x轴有两个交点,
∴△=b2﹣4ac>0,即4ac﹣b2<0,选项②正确;
③∵抛物线对称轴为x=﹣1,且x=0时,y>0,
∴当x=﹣2时,y=4a﹣2b+c>0,即4a+c>2b,选项③错误;
④∵抛物线对称轴x=﹣1,即﹣
 =﹣1,
=﹣1,
∴a=
 ,
,
由图象可知,当x=1时,y=a+b+c=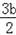
 +c<0,
+c<0,
故3b+2c<0,选项④正确;
⑤由图象可知,当x=﹣1时y取得最大值,
∵m≠﹣1,
∴am2+bm+c<a﹣b+c,即am2+bm+b<a,
∴m(am+b)+b<a,选项⑤正确;
故答案为:②④⑤.
【点评】主要考查图象与二次函数系数之间的关系,掌握二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定是解题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A.1,2,3 B.1,1,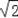
 C.1,1,
C.1,1,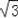
 D.1,2,
D.1,2,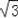

查看答案和解析>>
科目:初中数学 来源: 题型:
某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一次函数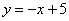 的图像与反比例函数
的图像与反比例函数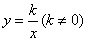 在第一象限内的图像交于
在第一象限内的图像交于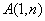 和
和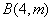 两点.
两点.
(1)求反比例函数的表达式;
|
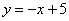 的值大于反比例函数
的值大于反比例函数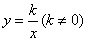 的值时,写出自变量
的值时,写出自变量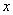 的取值范围.
的取值范围.
第20题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com