
【题目】如图,直线![]() ,
,![]() 与
与![]() ,
,![]() 分别相交于点
分别相交于点![]() ,
,![]() ,且
,且![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,
,![]() ,
,![]() ,求直线
,求直线![]() 与
与![]() 的距离.
的距离.
科目:初中数学 来源: 题型:
【题目】某校七年级为了表彰“数学素养水平测试”中表现优秀的同学,准备用480元钱购进笔记本作为奖品.若![]() 种笔记本买20本,
种笔记本买20本,![]() 本笔记本买30本,则钱还缺40元;若
本笔记本买30本,则钱还缺40元;若![]() 种笔记本买30本,
种笔记本买30本,![]() 种笔记本买20本,则钱恰好用完.
种笔记本买20本,则钱恰好用完.
(1)求![]() ,
,![]() 两种笔记本的单价.
两种笔记本的单价.
(2)由于实际需要,需要增加购买单价为6元的![]() 种笔记本若干本.若购买
种笔记本若干本.若购买![]() ,
,![]() ,
,![]() 三种笔记本共60本,钱恰好全部用完.任意两种笔记本之间的数量相差小于15本,则
三种笔记本共60本,钱恰好全部用完.任意两种笔记本之间的数量相差小于15本,则![]() 种笔记本购买了__________本.(直接写出答案)
种笔记本购买了__________本.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间福州一中初中部举行了“宅家运动会”.该学校七、八年级各有300名学生参加了这次“宅家运动会”,现从七、八年级各随机抽取20名学生宅家运动会的成绩进行抽样调查.
收集数据如下:
七年级: | 74 | 97 | 96 | 72 | 98 | 99 | 72 | 73 | 76 | 74 |
74 | 69 | 76 | 89 | 78 | 74 | 99 | 97 | 98 | 99 | |
八年级: | 76 | 88 | 96 | 89 | 78 | 94 | 89 | 94 | 95 | 50 |
89 | 68 | 65 | 89 | 77 | 86 | 89 | 88 | 92 | 91 |
整理数据如下:
|
|
|
|
| |
七年级 | 0 | 1 | 10 | 1 | a |
八年级 | 1 | 2 | 3 | 8 | 6 |
分析数据如下:
年级 | 平均数 | 中位数 | 众数 | 方差 |
七年级 | 84.2 | 77 | 74 | 138.56 |
八年级 | 84 | b | 89 | 129.7 |
根据以上信息,回答下列问题:
(1)![]() ___________,
___________,![]() ___________;
___________;
(2)你认为哪个年级“宅家运动会”的总体成绩较好,说明理由(至少从两个不同的角度说明推断的合理性)
(3)学校对“宅家运动会”成绩不低于80分的学生颁发优胜奖,请你估计学校七、八年级所有学生中获得优胜奖的大约有___________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且![]() ,弦AD的延长线交切线PC于点E,连接BC.
,弦AD的延长线交切线PC于点E,连接BC.
(1)判断OB和BP的数量关系,并说明理由;
(2)若⊙O的半径为2,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
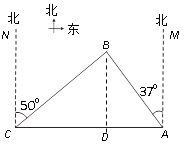
【题目】南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?
![]() (参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
(参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
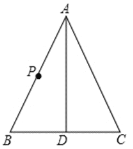
【题目】如图,在△ABC中,AB=AC, AD是△ABC 底边BC上的中线,P为AB上一点.
(1)在AD上找一点E,使得PE+EB的值最小;
(2)若P为AB的中点,当∠BPE= °时,△ABC是等边三角形.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=![]() ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.
,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com