练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某校七年级为了表彰“数学素养水平测试”中表现优秀的同学，准备用480元钱购进笔记本作为奖品.若种笔记本买20本，本笔记本买30本，则钱还缺40元；若种笔记本买30本，种笔记本买20本，则钱恰好用完.

    （1）求，两种笔记本的单价.

    （2）由于实际需要，需要增加购买单价为6元的种笔记本若干本.若购买，，三种笔记本共60本，钱恰好全部用完.任意两种笔记本之间的数量相差小于15本，则种笔记本购买了__________本.（直接写出答案）

    【答案】（1）、两种笔记本的单价分别为8元，12元；（2）24,26,28.

    【解析】

    （1）设、单价分别为，，根据题意列出方程组即可求解；

    （2）设种笔记本购买本，种笔记本购买本，得到方程组，根据任意两种笔记本之间的数量相差小于15本，得到b的取值，故可求解.

    解：（1）设、单价分别为，；

    ，解得，.

    （2）设种笔记本购买本，种笔记本购买本，

    故，解得，故

    ∵任意两种笔记本之间的数量相差小于15本，

    即，把、=2b,代入求得不等式组的解集为

    可知：，

    ∴b可以为12，13,14，

    对应的c为24,26,28.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在一节数学课上，老师出示了这样一个问题让学生探究：

    已知：如图在△ABC中，点D 是BA边延长线上一动点，点F 在BC上，且，连接DF交AC于点E .

    （1）如图1，当点E恰为DF的中点时，请求出的值；

    （2）如图2，当时，请求出的值（用含a的代数式表示）.

    思考片刻后，同学们纷纷表达自己的想法：

    甲：过点F作FG∥AB交AC于点G，构造相似三角形解决问题；

    乙：过点F作FG∥AC交AB于点G，构造相似三角形解决问题；

    丙：过点D作DG∥BC交CA延长线于点G，构造相似三角形解决问题；

    老师说：“这三位同学的想法都可以” .

    请参考上面某一种想法，完成第（1）问的求解过程，并直接写出第（2）问的值.

    图1 图2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，有一枚质地均匀的正二十面体形状的骰子，其中的1个面标有“1”，2个面标有“2”， 3个面标有“3”，4个面标有“4”，5个面标有“5”，其余的面标有“6”.将这枚骰子掷出后：

    （1）数字几朝上的概率最小？

    （2）奇数面朝上的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，过点C的直线m∥AB，D为AB边上一点，过点D作DE⊥BC，交直线m于点E，垂足为点F，连接CD，BE．

    （1）求证：CE=AD；

    （2）当点D是AB中点时，四边形BECD是什么特殊四边形？说明你的理由；

    （3）当∠A的大小满足什么条件时，四边形BECD是正方形？（不需要证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A（a，0）和B（0，b）满足（a﹣4）2+｜b﹣6｜＝0，分别过点A，B作x轴．y轴的垂线交于点C，如图所示．点P从原点出发，以每秒1个单位长度的速度沿着O→B→C→A的路线移动，运动时间为t秒．

    （1）写出A，B，C三点的坐标：A　 　，B　 　，C　 　；

    （2）当t＝14秒时，求△OAP的面积．

    （3）点P在运动过程中，当△OAP的面积为6时，求t的值及点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=BC，连接OE．下列结论：①∠CAD=30°；②SABCD=ABAC；③OB=AB；④OE=BC，成立的个数有（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，方格纸中每个小正方形的边长为1cm，平移图中的△ABC，使点B移到点B1的位置．

    （1）利用方格和直尺画图

    ①画出平移后的△A1B1C1

    ②画出AB边上的中线CD；

    ③画出BC边上的高AH；

    （2）线段A1C1与线段AC的位置关系与数量关系为　 　；

    （3）△A1B1C1的面积为　 　cm2；△BCD的面积为　 　cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（一）知识链接

    若点M，N在数轴上，且M，N代表的实数分别是a，b，则线段MN的长度可表示为 .

    （二）解决问题

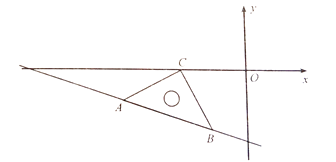
    如图，将一个三角板放置在平面直角坐标系中，∠ACB=90°，AC=BC，点B，C的坐标分别为（-2，-4），（-4，0）.

    （1）求点A的坐标及直线AB的表达式；

    （2）若P是x轴上一点，且S△ABP=6，求点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线，与，分别相交于点，，且，交直线于点.

    （1）若，求的度数；

    （2）若，，，求直线与的距离.

    查看答案和解析>>

    同步练习册答案