
【题目】(一)知识链接
若点M,N在数轴上,且M,N代表的实数分别是a,b,则线段MN的长度可表示为 .
(二)解决问题
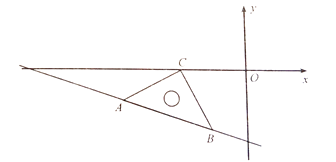
如图,将一个三角板放置在平面直角坐标系中,∠ACB=90°,AC=BC,点B,C的坐标分别为(-2,-4),(-4,0).
(1)求点A的坐标及直线AB的表达式;
(2)若P是x轴上一点,且S△ABP=6,求点P的坐标.
【答案】(一)![]() ;(二)(1)
;(二)(1)![]() ;
;![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(一)根据题意无法确定![]() 和
和![]() 的正负,因此线段MN的长度可表示为
的正负,因此线段MN的长度可表示为![]() ;
;
(二)(1)首先设点A的坐标为![]() ,根据已知条件列出二元一次方程组,解得即可;设直线AB的表达式为
,根据已知条件列出二元一次方程组,解得即可;设直线AB的表达式为![]() ,将A、B坐标代入即得解;
,将A、B坐标代入即得解;
(2)首先设点P的坐标为![]() ,
,![]() 的高为
的高为![]() ,根据
,根据![]() 的面积列出等式,即可解得.
的面积列出等式,即可解得.
解:(一)![]()
根据题意,无法确定![]() 和
和![]() 的正负,因此线段MN的长度可表示为
的正负,因此线段MN的长度可表示为![]() ;
;
(二)(1)设点A的坐标为![]()
∵∠ACB=90°,AC=BC,点B,C的坐标分别为(-2,-4),(-4,0)
∴![]()
∴![]()
∴![]() ,
,![]()
联立方程组,即为![]()
解得![]() 或
或![]() (A在第三象限,故舍去)
(A在第三象限,故舍去)
故点A坐标为![]() ;
;
设直线AB的表达式为![]() ,将A、B坐标代入即得
,将A、B坐标代入即得
![]()
解得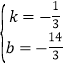
故AB的表达式为![]() .
.
(2)设点P的坐标为![]() ,
,![]() 的高为
的高为![]() ,
,
则![]() 即为点P到直线AB的距离,
即为点P到直线AB的距离,
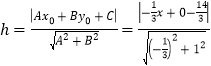 ①
①
又∵S△ABP=6,
∴![]()
∴![]() ②
②
联立①②,解得![]() 或
或![]()
故点P坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边三角形ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级为了表彰“数学素养水平测试”中表现优秀的同学,准备用480元钱购进笔记本作为奖品.若![]() 种笔记本买20本,
种笔记本买20本,![]() 本笔记本买30本,则钱还缺40元;若
本笔记本买30本,则钱还缺40元;若![]() 种笔记本买30本,
种笔记本买30本,![]() 种笔记本买20本,则钱恰好用完.
种笔记本买20本,则钱恰好用完.
(1)求![]() ,
,![]() 两种笔记本的单价.
两种笔记本的单价.
(2)由于实际需要,需要增加购买单价为6元的![]() 种笔记本若干本.若购买
种笔记本若干本.若购买![]() ,
,![]() ,
,![]() 三种笔记本共60本,钱恰好全部用完.任意两种笔记本之间的数量相差小于15本,则
三种笔记本共60本,钱恰好全部用完.任意两种笔记本之间的数量相差小于15本,则![]() 种笔记本购买了__________本.(直接写出答案)
种笔记本购买了__________本.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由:
如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.

证明:∵CD∥EF,
∴∠DCB=∠2( ),
∵∠1=∠2,
∴∠DCB=∠1( ).
∴GD∥CB( ),
∴∠3=∠ACB( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有若干个仅颜色不同的红球和黑球,现往一个不透明的袋子里装进4个红球和6个黑球.
(1)若先从袋子里取出m个红球(不放回),再从袋子里随机摸出一个球,将“摸到黑球”记为事件A. 若事件A为必然事件,则m= .
(2)若先从袋子里取出n个黑球,再放入2n个红球,若随机摸出一个球是红球的概率等于2/3,通过计算求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
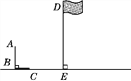
【题目】如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间福州一中初中部举行了“宅家运动会”.该学校七、八年级各有300名学生参加了这次“宅家运动会”,现从七、八年级各随机抽取20名学生宅家运动会的成绩进行抽样调查.
收集数据如下:
七年级: | 74 | 97 | 96 | 72 | 98 | 99 | 72 | 73 | 76 | 74 |
74 | 69 | 76 | 89 | 78 | 74 | 99 | 97 | 98 | 99 | |
八年级: | 76 | 88 | 96 | 89 | 78 | 94 | 89 | 94 | 95 | 50 |
89 | 68 | 65 | 89 | 77 | 86 | 89 | 88 | 92 | 91 |
整理数据如下:
|
|
|
|
| |
七年级 | 0 | 1 | 10 | 1 | a |
八年级 | 1 | 2 | 3 | 8 | 6 |
分析数据如下:
年级 | 平均数 | 中位数 | 众数 | 方差 |
七年级 | 84.2 | 77 | 74 | 138.56 |
八年级 | 84 | b | 89 | 129.7 |
根据以上信息,回答下列问题:
(1)![]() ___________,
___________,![]() ___________;
___________;
(2)你认为哪个年级“宅家运动会”的总体成绩较好,说明理由(至少从两个不同的角度说明推断的合理性)
(3)学校对“宅家运动会”成绩不低于80分的学生颁发优胜奖,请你估计学校七、八年级所有学生中获得优胜奖的大约有___________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
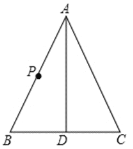
【题目】如图,在△ABC中,AB=AC, AD是△ABC 底边BC上的中线,P为AB上一点.
(1)在AD上找一点E,使得PE+EB的值最小;
(2)若P为AB的中点,当∠BPE= °时,△ABC是等边三角形.(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com