
【题目】如图,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边三角形ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;

【答案】BD存在最大值,最大值是6.
【解析】
以AD为边做作等边三角形ADE,连接CE,根据等边三角形的性质和全等三角形的判定证明△ABD≌△ACE,再利用全等三角形的性质以及两点之间线段最短,即可证得结论.
证明:BD存在最大值;
如图,以AD为边做作等边三角形ADE,连接CE,
∵△ABC、△ADE都是等边三角形,
∴AB=AC,AD=AE=DE=2,∠BAC=∠EAD=60°,
∵∠BAD=∠BAC+∠DAC,∠EAC=∠EAD+∠DAC
∴∠BAD=∠EAC,且AB=AC,AD=AE
∴△ABD≌△ACE
∴BD=CE
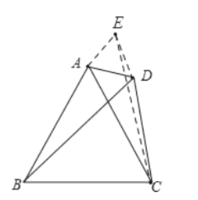
若点E,点D,点C不在一条直线上,则EC<ED+DC;
若点E,点D,点C在一条直线上,则EC=ED+DC.
∴EC≤ED+CD=2+4=6
∴BD≤6,
∴BD存在最大值,最大值是6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某餐厅以![]() 、
、![]() 两种食材,利用不同的搭配方式推出了两款健康餐,其中,甲产品每份含200克
两种食材,利用不同的搭配方式推出了两款健康餐,其中,甲产品每份含200克![]() 、200克
、200克![]() ;乙产品每份含200克
;乙产品每份含200克![]() 、100克
、100克![]() .甲、乙两种产品每份的成本价分别为
.甲、乙两种产品每份的成本价分别为![]() 、
、![]() 两种食材的成本价之和,若甲产品每份成本价为16元.店家在核算成本的时候把
两种食材的成本价之和,若甲产品每份成本价为16元.店家在核算成本的时候把![]() 、
、![]() 两种食材单价看反了,实际成本比核算时的成本多688元,如果每天甲销量的4倍和乙销量的3倍之和不超过120份,那么餐厅每天实际成本最多为______元.
两种食材单价看反了,实际成本比核算时的成本多688元,如果每天甲销量的4倍和乙销量的3倍之和不超过120份,那么餐厅每天实际成本最多为______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学课上,老师出示了这样一个问题让学生探究:
已知:如图在△ABC中,点D 是BA边延长线上一动点,点F 在BC上,且![]() ,连接DF交AC于点E .
,连接DF交AC于点E .
(1)如图1,当点E恰为DF的中点时,请求出![]() 的值;
的值;
(2)如图2,当![]() 时,请求出
时,请求出![]() 的值(用含a的代数式表示).
的值(用含a的代数式表示).
思考片刻后,同学们纷纷表达自己的想法:
甲:过点F作FG∥AB交AC于点G,构造相似三角形解决问题;
乙:过点F作FG∥AC交AB于点G,构造相似三角形解决问题;
丙:过点D作DG∥BC交CA延长线于点G,构造相似三角形解决问题;
老师说:“这三位同学的想法都可以” .
请参考上面某一种想法,完成第(1)问的求解过程,并直接写出第(2)问![]() 的值.
的值.


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,以下四个结论:①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC,其中一定正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班在商场购买甲、乙两种不同的书籍,购买甲种书籍共花费2600元,购买乙种书籍共花费1328元,购买甲种书籍的数量是购买乙种书籍数量的2.5倍,且购买一个乙种书籍比购买一个甲种书籍多花18元.求购买一个甲种书籍、一个乙种书籍各需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,那么锻造的操作时间有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一枚质地均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”, 3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这枚骰子掷出后:

(1)数字几朝上的概率最小?
(2)奇数面朝上的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD,BE.
(1)求证:CE=AD;
(2)当点D是AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)当∠A的大小满足什么条件时,四边形BECD是正方形?(不需要证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(一)知识链接
若点M,N在数轴上,且M,N代表的实数分别是a,b,则线段MN的长度可表示为 .
(二)解决问题
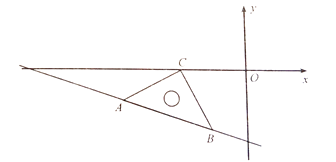
如图,将一个三角板放置在平面直角坐标系中,∠ACB=90°,AC=BC,点B,C的坐标分别为(-2,-4),(-4,0).
(1)求点A的坐标及直线AB的表达式;
(2)若P是x轴上一点,且S△ABP=6,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com