
【题目】如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,以下四个结论:①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC,其中一定正确的是_____.

科目:初中数学 来源: 题型:
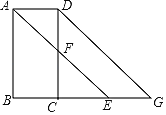
【题目】如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,DG交BC的,延长线于G,∠CFE=∠AEB
(1)若∠B=87°,求∠DCG的度数;
(2)AD与BC是什么位置关系?并说明理由;
(3)若∠DAB=α,∠DGC=β,直接写出α、β满足什么数量关系时,AE∥DG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线 y1=kx+b 经过点 P(4,4)和点 Q(0,﹣4),与 x 轴交于点 A,与直线 y2=mx+n 交于点 P.
(1)求出直线 y1=kx+b 的解析式;
(2)求出点 A 的坐标;
(3)直线 y2=mx+n 绕着点 P 任意旋转,与 x 轴交于点 B,当△PAB 是等腰三角形时,直接写出点B 的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量分别为45人/辆和30人/辆和租金分比为400元/辆和280元/辆:杏坛中学根据实际情况,计划租用A,B型客车共5辆,同时送八年级师生到基地参加社会实践活动,若要保证租车费用不超过1900元,求A型客车的数量最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边三角形ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=![]() (x>0)相交于P(1,m).
(x>0)相交于P(1,m).
(1)求k的值;
(2)若点Q与点P关于y=x成轴对称,则点Q的坐标为Q( );
(3)若过P、Q两点的抛物线与y轴的交点为N(0, ![]() ),求该抛物线的解析式,并求出抛物线的对称轴方程.
),求该抛物线的解析式,并求出抛物线的对称轴方程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由:
如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.

证明:∵CD∥EF,
∴∠DCB=∠2( ),
∵∠1=∠2,
∴∠DCB=∠1( ).
∴GD∥CB( ),
∴∠3=∠ACB( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com