【题目】解不等式（组），并在数轴上表示它的解集
（1）2（1+x）＜3；
（2）
.
科目：初中数学 来源： 题型：
【题目】完成下面的证明：
已知：如图，点D、E、F分别在线段AB、BC、AC上，连接DE、EF、DM平分∠ADE交EF于点M，
，求证：
。
证明：（已知）
又
（平角定义）
∴∠2=∠BEM（____________________）
∴
__________（_________________________）
（_____________________________）
（_____________________________）
又∵DM平分∠ADE（已知）
（角平分线定义）
（等量代换）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某餐厅以
、
两种食材，利用不同的搭配方式推出了两款健康餐，其中，甲产品每份含200克、200克；乙产品每份含200克、100克．甲、乙两种产品每份的成本价分别为、两种食材的成本价之和，若甲产品每份成本价为16元．店家在核算成本的时候把、两种食材单价看反了，实际成本比核算时的成本多688元，如果每天甲销量的4倍和乙销量的3倍之和不超过120份，那么餐厅每天实际成本最多为______元．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图 AB=AC，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点O．
（1）求证AD=AE；
（2）连接OA，BC，试判断直线OA，BC的关系并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，E为AD边上的一点，过C点作CF⊥CE交AB的延长线于点F.
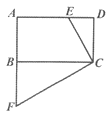
（1）求证：△CDE∽△CBF；
（2）若B为AF的中点，CB=3，DE=1，求CD的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一位农民带上若干千克自产的土豆进城出售．为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出的土豆千克数与他手中持有的钱数（含备用零钱）的关系，如图，结合图象回答下列问题：
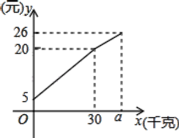
（1）农民自带的零钱是多少？
（2）求出降价前每千克的土豆价格是多少？
（3）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，试问他一共带了多少千克土豆？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一节数学课上，老师出示了这样一个问题让学生探究：
已知：如图在△ABC中，点D 是BA边延长线上一动点，点F 在BC上，且
，连接DF交AC于点E .
（1）如图1，当点E恰为DF的中点时，请求出
的值；
（2）如图2，当
时，请求出
的值（用含a的代数式表示）.
思考片刻后，同学们纷纷表达自己的想法：
甲：过点F作FG∥AB交AC于点G，构造相似三角形解决问题；
乙：过点F作FG∥AC交AB于点G，构造相似三角形解决问题；
丙：过点D作DG∥BC交CA延长线于点G，构造相似三角形解决问题；
老师说：“这三位同学的想法都可以” .
请参考上面某一种想法，完成第（1）问的求解过程，并直接写出第（2）问
的值.
图1 图2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B的对应点为E，连接BE，以下四个结论：①AC＝AD；②AB⊥EB；③BC＝EC；④∠A＝∠EBC，其中一定正确的是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=90°，过点C的直线m∥AB，D为AB边上一点，过点D作DE⊥BC，交直线m于点E，垂足为点F，连接CD，BE．
（1）求证：CE=AD；
（2）当点D是AB中点时，四边形BECD是什么特殊四边形？说明你的理由；
（3）当∠A的大小满足什么条件时，四边形BECD是正方形？（不需要证明）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
