[题目]已知x=1是关于x的方程ax+b=c的解.则2的值为( )A. 0B. 1C. 2D. 3 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】已知x=1是关于x的方程ax+b=c的解，则(a+b-c)2的值为（）

A. 0B. 1C. 2D. 3

【答案】A

【解析】

把x=1代入方程ax+b=c，可得a+b=c，然后代入(a+b-c)2计算即可.

把x=1代入方程ax+b=c，得a+b=c

∴(a+b-c)2=(c-c)2=0.

故选A.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】在数学活动课上，同学们判断一个四边形门框是否为矩形.下面是某学习小组4位同学拟定的方案，其中正确的是

A. 测量对角线是否平分 B. 测量两组对边是否分别相等

C. 测量其中三个角是否是直角 D. 测量对角线是否相等

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】两组邻边分别相等的四边形叫做筝形.如图1，四边形ABCD是一个筝形，其中AD=CD，AB=CB，我们称这个四边形是“筝形ABCD”.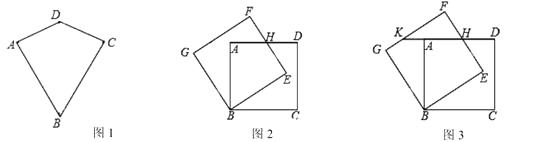

（1）根据筝形的定义判断下列命题是否正确，真命题打“√”，假命题打“×”.
①筝形有一组对角相等.
②菱形是筝形.
③筝形的面积为两条对角线长度的乘积.
（2）如图2，有一个公共顶点B的两个正方形ABCD与正方形BEFG全等，边AD与EF相交于点H.请你判断四边形BEHA是否是“筝形”，说明你的理由；
（3）如图3，当∠EBC=30°时，延长DA交GF于点K.若正方形ABCD边长为，求线段AK的长.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，矩形ABCD中，对角线AC、BD相交于点O，过点O作OE⊥BD交AD于点E．已知AB=2，△DOE的面积为，则AE的长为（）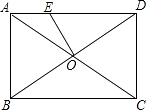
A.
B.2
C.1.5
D.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，四边形ABCD的对角线AC、BD相交于点O，分别作BE⊥AC于E，DF⊥AC于F，已知OE=OF，CE=AF．

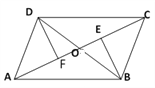
（1）求证：△BOE≌△DOF；

（2）若，则四边形ABCD是什么特殊四边形？请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】对一批衬衣进行抽检，得到合格衬衣的频数表如下，若出售1200件衬衣，则其中次品的件数大约是（）

抽取件数（件）	50	100	150	200	500	800	1000
合格频数	48	98	144	193	489	784	981

A.12B.24C.1188D.1176

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】∠1与∠2是内错角，∠1=50°，则∠2的度数为 ( )

A. 50°B. 130°C. 50°或130°D. 不能确定

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如果一个角的两边分别平行于另一个角的两边，且其中一个角是55°，则另一个角的度数为 ______。

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在数轴上，把表示数1的点称为基准点，记作点. 对于两个不同的M和N，若点M、点N到点的距离相等，则称点M与点N互为基准变换点. 例如：图中，点M表示数，点N表示数3，它们与基准点的距离都是2个单位长度，点M与点N互为基准变换点.

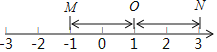
（1）已知点A表示数a，点B表示数b，点A与点B互为基准变换点.

① 若a=0，则b= ；若，则b= ；

② 用含a的式子表示b，则b= ；

（2）对点A进行如下操作：先把点A表示的数乘以，再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点，则点A表示的数是；

（3）点P在点Q的左边，点P与点Q之间的距离为8个单位长度．对P、Q两点做如下操作：点P沿数轴向右移动k（k>0）个单位长度得到，为的基准变换点，点沿数轴向右移动k个单位长度得到，为的基准变换点，……,依此顺序不断地重复，得到，，…， . 为Q的基准变换点,将数轴沿原点对折后的落点为，为的基准变换点, 将数轴沿原点对折后的落点为，……，依此顺序不断地重复，得到，，…， .若无论k为何值，与两点间的距离都是4，则n= .

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学