
 抛物线y=x2+4ax+b与x轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
抛物线y=x2+4ax+b与x轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.分析 (1)令a=$\frac{3}{2}$代入抛物线,由于抛物线过原点,所以b=0,从而求出抛物线的解析式,然后根据条件求出点B与C的坐标即可求出BC的长度.
(2)由题意可知b=0,然后根据P的坐标分别求出A、B、C、M的坐标,进而求出BC、BP、PM、AM的长度,最后利用△AMP∽△BPC列出关于a的方程即可求出a的值.
解答 解:(1)当a=$\frac{3}{2}$时,
∴抛物线为:y=x2+6x+b,
∴对称轴为x=-3,
又∵抛物线过原点,
∴b=0,
∴y=x2+6x,
∴令x=2代入y=x2+6x,
∴y=16,
∴B(2,16),
∵点B关于抛物线对称轴的对称点为C,
∴C(-8,16),
∴BC=2-(-8)=10,
(2)由于抛物线过原点O,
∴b=0,
∴y=x2+4ax,
令x=2代入y=x2+4ax,
∴y=4+8a,
∴B(2,4+8a),
∵∵点B关于抛物线对称轴的对称点为C,
抛物线的对称轴为x=-2a,
∴C(-4a-2,4+8a),
∵O与A关于x=-2a对称,
∴A(-4a,0),
∴BC=-4a-2-2=-4a-4,
∵P(2,2a),
∴M(2,0),
∴PM=0-2a=-2a,AM=-4a-2,
BP=2a-(4+8a)=-4-6a,
∵AP⊥PC,
∴∠APM=∠PCB,
∴△AMP∽△BPC,
∴$\frac{BP}{AM}=\frac{BC}{PM}$,
∴$\frac{-4-6a}{-4a-2}$=$\frac{-4a-4}{-2a}$,
∴a=-2$±\sqrt{2}$,
∵a<-1,
∴a=-2-$\sqrt{2}$
点评 本题考查二次函数综合问题,涉及相似三角形的判定与性质,一元二次方程的解法,待定系数求解析式等知识,知识较为综合,属于中等题型.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
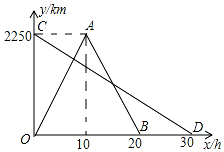 一辆快车和一辆慢车分别从甲、乙两地同时出发匀速相向而行,快车到达乙地后,原路原速返回甲地.图1表示两车行驶过程中离甲地的路程y(km)与行驶时间x(h)的函数图象.
一辆快车和一辆慢车分别从甲、乙两地同时出发匀速相向而行,快车到达乙地后,原路原速返回甲地.图1表示两车行驶过程中离甲地的路程y(km)与行驶时间x(h)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,有一点C,过点C分别作CA⊥x轴,CB⊥y轴,点A、B是垂足.
在平面直角坐标系xOy中,有一点C,过点C分别作CA⊥x轴,CB⊥y轴,点A、B是垂足.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,边长为a,面积为2的正方形放置在数轴上,以原点为圆心,a为半径,在原点右侧用圆规画出数轴上的一个点A,则点A所表示的实数是$\sqrt{2}$.
如图,边长为a,面积为2的正方形放置在数轴上,以原点为圆心,a为半径,在原点右侧用圆规画出数轴上的一个点A,则点A所表示的实数是$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 单项式-34a2b5的次数是11次 | |
| B. | 已知a是有理数,且|a|=-a,则有理数a在数轴上的对应点在原点的左边 | |
| C. | 无理数的绝对值一定是非负数 | |
| D. | 延长线段BA到C,使AC=2BC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com