
【题目】在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的个数是( )
①AC⊥DE;②![]() =
=![]() ;③CD=2DH;④
;③CD=2DH;④![]() .
.

A.1B.2C.3D.4
【答案】C
【解析】
试题分析:∵AD∥BC,∠ABC=90°
∴∠BAD=90°,
又∵AB=BC,
∴∠BAC=45°,
∴∠CAD=∠BAD﹣∠BAC=90°﹣45°=45°,
∴∠BAC=∠CAD,
∴AH⊥ED,
即AC⊥ED,故①正确;
∵△CHE为直角三角形,且∠HEC=60°
∴EC=2EH
∵∠ECB=15°,
∴EC≠4EB,
∴EH≠2EB;故②错误.
∵由证①中已知,∠BAC=∠CAD,
在△ACD和△ACE中,
 ,
,
∴△ACD≌△ACE(SAS),
∴CD=CE,
∵∠BCE=15°,
∴∠BEC=90°﹣∠BCE=90°﹣15°=75°,
∴∠CED=180°﹣∠BEC﹣∠AED=180°﹣75°﹣45°=60°,
∴△CDE为等边三角形,
∴∠DCH=30°,
∴CD=2DH,故③正确;
过H作HM⊥AB于M,
∴HM∥BC,
∴△AMH∽△ABC,
∴![]() ,
,
∵∠DAC=∠ADH=45°,
∴DH=AH,
∴![]() ,
,
∵△BEH和△CBE有公共底BE,
∴![]() ,故④正确,
,故④正确,
∴结论正确的个数是3.
故选C.



科目:初中数学 来源: 题型:
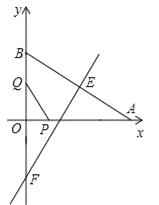
【题目】如图,在Rt△AOB中,∠AOB=90°,AO=![]() ,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F,点P从点A出发沿射线AO以每秒2
,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F,点P从点A出发沿射线AO以每秒2![]() 个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动,设运动的时间为t秒.
个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动,设运动的时间为t秒.
(1)①当t为何值时,PQ∥AB;②当t为何值时,PQ∥EF;
(2)当点P在O的左侧时,记四边形PFEQ的面积为S,求S关于t的函数关系式;
(3)以O为原点,OA所在直线为x轴,建立直角坐标系,若P、Q关于点O的对称点分别为P′、Q′,当线段P′Q′,与线段EF有公共点时,抛物线y=ax2+1经过P′Q′的中点,此时的抛物线与x正半轴交于点M;
①求a的取值范围;
②求点M移动的运动速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一组数据x1,x2,…xn的平均数是2,方差是1,则3x1+2,3x2+2,…+3xn+2的平均数和方差分别是( )
A. 2,1 B. 8,1 C. 8,5 D. 8,9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车每个运行班次的载客量,得到如下频数分布直方图.如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题.

(1)找出这天载客量的中位数,说明这个中位数的意义;
(2)估计3路公共汽车平均每班的载客量大约是多少?
(3)计算这天载客量在平均载客量以上班次占总班次的百分数.
(注:一个小组的组中值是指这个小组的两个端点数的平均数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列式子可以用“=”连接的是( )
A. 5+4_______12-5 B. 7+(-4)______7-(+4)
C. 2+4(-2)______-12 D. 2(3-4)_____23-4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com