
【题目】(10分)在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE=![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图1).求证:△BOG≌△POE;
(2)结合图2,通过观察、测量、猜想:![]() =______,并证明你的猜想;
=______,并证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图3),若AC=8,BD=6,直接写出![]() 的值.
的值.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据正方形的性质证得OB="OP" , ∠BOC=∠BOG=90°,利用互余的性质证得∠GBO=∠EPO ,然后根据AAS可证明△BOG≌△POE;(2)过P作PM//AC交BG于M,交BO于N,根据条件证明△BMN≌△PEN,得出BM=PE,然后根据条件证明△BPF≌△MPF,得出BF="MF" ,然后可求![]() ;(3)类比(2)的解题方法可得出结论.
;(3)类比(2)的解题方法可得出结论.
试题解析:解:(1)证明:∵四边形ABCD是正方形,P与C重合,
∴OB="OP" , ∠BOC=∠BOG=90°.
∵PF⊥BG ,∠PFB=90°,
∴∠GBO=90°-∠BGO,∠EPO=90°-∠BGO.
∴∠GBO=∠EPO . .3分
∴△BOG≌△POE(AAS). .4分
(2)![]() . ..5分
. ..5分
证明如下:
如图,过P作PM//AC交BG于M,交BO于N,
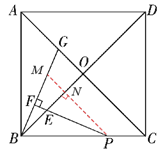
∴∠PNE=∠BOC=90°,∠BPN=∠OCB.
∵∠OBC=∠OCB =45°,∴ ∠NBP=∠NPB,∴NB=NP.
∵∠MBN=90°-∠BMN,∠NPE=90°-∠BMN,∴∠MBN=∠NPE.
∴△BMN≌△PEN(ASA),∴BM=PE.
∵∠BPE=![]() ∠ACB,∠BPN=∠ACB,∴∠BPF=∠MPF.
∠ACB,∠BPN=∠ACB,∴∠BPF=∠MPF.
∵PF⊥BM,∴∠BFP=∠MFP=90°.
又∵PF=PF, ∴△BPF≌△MPF(ASA).
∴BF="MF" ,即BF=![]() BM.
BM.
∴BF=![]() PE, 即
PE, 即![]() .. ..8分
.. ..8分
(3)![]() .. ..10分 (说明:用其它方法得到结果请相应给分)
.. ..10分 (说明:用其它方法得到结果请相应给分)


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的动点,BC∥OP,BC=OP.
(1)求证:四边形AOCP是平行四边形;
(2)若AB=4,填空:
①当AP= 时,四边形AOCP是菱形;
②当AP= 时,四边形OBCP是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t=![]() 或
或![]() .
.
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的个数是( )
①单独一个数0不是单项式;②单项式-a的次数为0;③多项式-a2+abc+1是二次三项式;④-a2b的系数是1.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、B、C、D四个点,其中横坐标x与纵坐标y的对应值如下表:
A | B | C | D | |
x | -1 | 0 | 1 | 3 |
y | -1 | 3 | 5 | 3 |
(1)求二次函数解析式;
(2)求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,BC边上有10个不同的点 ![]() ,
, ![]() ,……
,…… ![]() , 记
, 记 ![]() (i = 1,2,……,10),那么
(i = 1,2,……,10),那么 ![]() 的值为( )
的值为( )
A.4
B.14
C.40
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com