
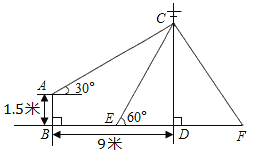
【题目】如图,电力公司在电线杆上的C处引两条等长的拉线CE、CF固定电线杆CD,拉线CE和地面成60°角,在离电线杆9米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米.
(1)求CD的长(结果保留根号);
(2)求EF的长(结果保留根号).
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)过点A作AH⊥CD,垂足为H,根据矩形的性质和直角三角形的性质可求解;
(2)在上面基础上,先证得△CEF是等边三角形,然后再根据直角三角形的性质求解.
试题解析:(1)过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=9,
在Rt△ACH中,tan∠CAH=![]() ,
,
∴CH=AH tan∠CAH,
∴CH=AH·tan∠CAH=9tan30°=9×![]() (米),
(米),
∵DH=1.5,
∴CD的长=![]() (米)
(米)
(2)在Rt△CDE中,
∵∠CED=60°,sin∠CED=![]() ,
,
∴CE=![]() =6+
=6+![]() 米,
米,
∴EF=CE=![]() (米)
(米)


科目:初中数学 来源: 题型:
【题目】小明和同桌小聪在课后复习时,对下面的一道思考题进行了认真的探索.
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时点B到墙AC的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动________米.
解完【思考题】后,小聪提出了如下两个问题:
(1)在【思考题】中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(2)在【思考题】中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
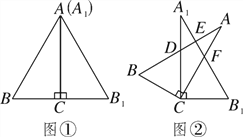
【题目】将两块相同的含30°角的直角三角板按图①的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图②的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
(1)当旋转角等于20°时,∠BCB1=________度;
(2)当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
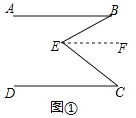
【题目】![]() 问题发现:如图
问题发现:如图![]() ,直线
,直线![]() 是AB与AD之间的一点,连接
是AB与AD之间的一点,连接![]() ,可以发现
,可以发现![]() .
.

请把下面的证明过程补充完整:
证明:过点E作![]() ,
,
![]() 已知
已知![]() 辅助线的作法
辅助线的作法![]() .
.
![]() _____
_____![]()
![]() ______
______
![]() 同理
同理![]() .
.
![]() _____
_____![]()
等量代换![]()
即![]() .
.
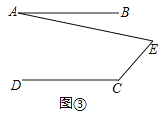
![]() 拓展探究:如果点E运动到图
拓展探究:如果点E运动到图![]() 所示的位置,其他条件不变,进一步探究发现:
所示的位置,其他条件不变,进一步探究发现: ![]() ,请说明理由.
,请说明理由.
![]() 解决问题:如图
解决问题:如图![]() ,请直接写出
,请直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
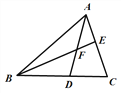
【题目】如图, ![]() ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
①S△ABD=S△DCA;② S△AEF=S△BDF;③S四边形EFDC=2S△AEF;④S△ABC=3S△ABF
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=![]() ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )

A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在对第一章“丰富的图形世界”复习前,老师让学生整理正方体截面的形状并探究多面体(由若干个多边形所围成的几何体)的棱数、面数、顶点数之间的数量关系,如图是小颖用平面截正方体后剩余的多面体,请解答下列问题:

(1)根据上图完成下表:
多面体 | V(顶点数) | F(面数) | E(棱数) |
(1) |
| 7 | 15 |
(3) | 6 |
| 9 |
(5) | 8 | 6 |
|
(2)猜想:一个多面体的V(顶点数),F(面数),E(棱数)之间的数量关系是 ;
(3)计算:已知一个多面体有20个面、30条棱,那么这个多面体有 个顶点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=![]() 的图象交于A,B两点,则四边形MAOB的面积为____________.
的图象交于A,B两点,则四边形MAOB的面积为____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com