
【题目】小明和同桌小聪在课后复习时,对下面的一道思考题进行了认真的探索.
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时点B到墙AC的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动________米.
解完【思考题】后,小聪提出了如下两个问题:
(1)在【思考题】中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(2)在【思考题】中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:

甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | |||
乙 | 1 |
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁将胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点![]() 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图

① ∵![]()
∴ ______// _____(______________________)
② ∵∠DAB+∠ABC=180°
∴ _____// _____(__________________)
③∵ AB // CD
∴∠_____+∠ABC=180°(___________________)
④∵ ______// ______
∴∠C=∠3(_______________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合.无论折叠多少次,只要最后一次恰好重合,我们就称∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿△ABC的∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
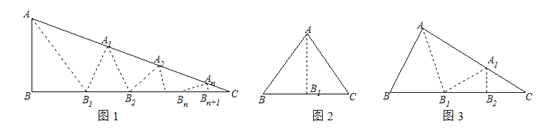
(1)小丽经过三次折叠发现了∠BAC是△ABC的好角,请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系.
(2)根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 ;
(3)如果一个三角形的最小角是15°,且满足该三角形的三个角均是此三角形的好角,则此三角形另两个角的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
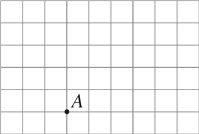
【题目】在如图所示的网格中,每个小正方形的边长都为1.
(1)试作出直角坐标系,使点A的坐标为(2,-1);
(2)在(1)中建立的直角坐标系中描出点B(3,4),C(0,1),并求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
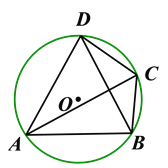
【题目】如图,在⊙O的内接四边形ABCD中,∠BCD=120°,AC平分∠BCD.
(1)求证:△ABD是等边三角形;
(2)若BD=6cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2015秒时,点P的坐标是( )
个单位长度,则第2015秒时,点P的坐标是( )
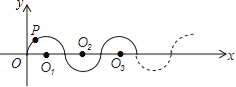
A. (2014,0) B. (2015,﹣1) C. (2015,1) D. (2016,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
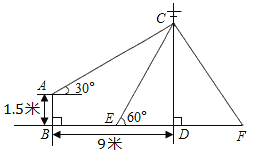
【题目】如图,电力公司在电线杆上的C处引两条等长的拉线CE、CF固定电线杆CD,拉线CE和地面成60°角,在离电线杆9米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米.
(1)求CD的长(结果保留根号);
(2)求EF的长(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com