练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图

    ① ∵

    ∴ ______// _____（______________________）

    ②　∵∠DAB+∠ABC=180°

    ∴ _____// _____（__________________）

    ③∵ AB // CD

    ∴∠_____+∠ABC=180°（___________________）

    ④∵ ______// ______

    ∴∠C=∠3（_______________________）

    【答案】 AB CD 内错角相等，两直线平行 AD BC 同旁内角互补，两直线平行 C 两直线平行，同旁内角互补 AD BC 两直线平行，内错角相等

    【解析】整体分析：

    利用平行线的性质和判定填空.

    解：① ∵

    ∴ AB//CD（内错角相等，两直线平行）

    ②∵∠DAB+∠ABC=180°

    ∴AD//BC（同旁内角互补，两直线平行）

    ③∵ AB // CD

    ∴∠C+∠ABC=180°（两直线平行，同旁内角互补）

    ④∵AD//BC

    ∴∠C=∠3（两直线平行，内错角相等）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（6分）在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球，它们除颜色外完全相同，其中红球有2个，黄球有1个，蓝球有1个.现有一张电影票，小明和小亮决定通过摸球游戏定输赢（赢的一方得电影票）．游戏规则是：两人各摸1次球，先由小明从纸箱里随机摸出1个球，记录颜色后放回，将小球摇匀，再由小亮随机摸出1个球并记录颜色．若两人摸到的球颜色相同，则小明赢，否则小亮赢．这个游戏规则对双方公平吗？请你利用树状图或列表法说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：

    对于平面图形A，如果存在一个圆，使图形A上的任意一点到圆心的距离都不大于这个圆的半径，则称图形A被这个圆所覆盖.

    对于平面图形A，如果存在两个或两个以上的圆，使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径，则称图形A被这些圆所覆盖.

    例如：图1中①的三角形被一个圆覆盖，②中的四边形被两个圆所覆盖.

    回答下列问题：

    (1)边长为1 cm的正方形被一个半径为r的圆所覆盖，r的最小值是______ cm;

    (2)边长为1 cm的等边三角形被一个半径为r的圆所覆盖，r的最小值是_____ cm;

    (3)长为2 cm，宽为1 cm的矩形被两个半径均为r的圆所覆盖，r的最小值是_____ cm.这两个圆的圆心距是_____ cm.。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某小区内有一块长、宽比为2∶1的矩形空地，计划在该空地上修筑两条宽均为2 m的互相垂直的小路，余下的四块小矩形空地铺成草坪，如果四块草坪的面积之和为312 m2，请求出原来大矩形空地的长和宽．

    (1)请找出上述问题中的等量关系：_________________；

    (2)若设大矩形空地的宽为xm，可列出的方程为_____________，方程的解为__________，原来大矩形空地的长和宽分别为_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店第一次用600元购进2B铅笔若干支，第二次又用600元购进该款铅笔，但这次每支的进价是第一次进价的倍，购进数量比第一次少了30支．

    （1）求第一次每支铅笔的进价是多少元？

    （2）若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元，问每支售价至少是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有边长分别为a，b的正方形Ⅰ号和Ⅱ号，以及长为a，宽为b的长方形Ⅲ号卡片足够多，我们可以选取适量的卡片拼接成几何图形．（卡片间不重叠、无缝隙）

    尝试解决：（1）图1是由1张Ⅰ号卡片、1张Ⅱ号卡片、2张Ⅲ号卡片拼接成的正方形，那么这个几何图形表示的等式是 ；

    （2）小聪想用几何图形表示等式（a+b）（2a+b）=2a2+3ab+b2，图2给出了他所拼接的几何图形的一部分，请你补全图形；

    （3）小聪选取1张Ⅰ号卡片、3张Ⅱ号卡片、4张Ⅲ号卡片拼接成一个长方形，那么拼接的几何图形表示的等式是 ；

    拓展研究：

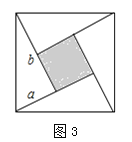
    （4）如图3，大正方形的边长为m，小正方形的边长为n，若用m、n表示四个直角三角形的两直角边边长（b＞a），观察图案，以下关系式中正确的有 ．（填写序号）

    ①ab=；②a+b=m；③a2+b2=m2；④a2+b2=．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明和同桌小聪在课后复习时，对下面的一道思考题进行了认真的探索．

    【思考题】如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时点B到墙AC的距离为0.7米，如果梯子的顶端沿墙下滑0.4米，那么点B将向外移动________米．

    解完【思考题】后，小聪提出了如下两个问题：

    (1)在【思考题】中，将“下滑0.4米”改为“下滑0.9米”，那么该题的答案会是0.9米吗？为什么？

    (2)在【思考题】中，梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离，有可能相等吗？为什么？

    请你解答小聪提出的这两个问题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

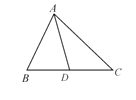
    【题目】如图所示，AD是△ABC的边BC的中线.

    (1)画出以点D为对称中心，与△ABD成中心对称的三角形；

    (2)若AB=10，AC=12，求AD长的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

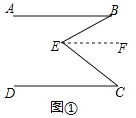
    【题目】问题发现：如图，直线是AB与AD之间的一点，连接，可以发现．

    请把下面的证明过程补充完整：

    证明：过点E作，

    已知辅助线的作法．

    _____

    ______

    同理．

    _____

    等量代换

    即．

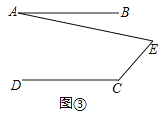
    拓展探究：如果点E运动到图所示的位置，其他条件不变，进一步探究发现： ，请说明理由．

    解决问题：如图，请直接写出的度数．

    查看答案和解析>>

    同步练习册答案