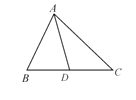
【题目】如图所示，AD是△ABC的边BC的中线.
(1)画出以点D为对称中心，与△ABD成中心对称的三角形；
(2)若AB=10，AC=12，求AD长的取值范围.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】阅读解题过程,回答问题.
如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数.
解:过O点作射线OM,使点M,O,A在同一直线上.
因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,所以∠BOC=∠MOD,
所以∠AOD=180°-∠BOC=180°-30°=150°.
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图
① ∵
∴ ______// _____（______________________）
② ∵∠DAB+∠ABC=180°
∴ _____// _____（__________________）
③∵ AB // CD
∴∠_____+∠ABC=180°（___________________）
④∵ ______// ______
∴∠C=∠3（_______________________）
查看答案和解析>>
科目：初中数学 来源： 题型：
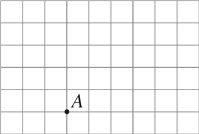
【题目】在如图所示的网格中，每个小正方形的边长都为1.
(1)试作出直角坐标系，使点A的坐标为(2，－1)；
(2)在(1)中建立的直角坐标系中描出点B(3，4)，C(0，1)，并求三角形ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
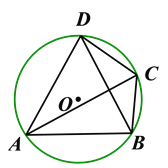
【题目】如图，在⊙O的内接四边形ABCD中，∠BCD=120°，AC平分∠BCD.
(1)求证：△ABD是等边三角形；
(2)若BD=6cm，求⊙O的半径.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明利用灯光下自己的影子长度来测量路灯的高度．如图，CD和EF是两等高的路灯，相距27m，身高1.5m的小明（AB）站在两路灯之间（D、B、F共线），被两路灯同时照射留在地面的影长BQ=4m，BP=5m．
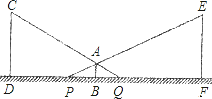
(1)小明距离路灯多远？
(2)求路灯高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒
个单位长度，则第2015秒时，点P的坐标是（ ）
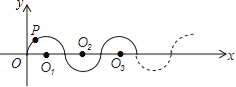
A. （2014，0） B. （2015，﹣1） C. （2015，1） D. （2016，0）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，BC∥OA，∠B＝∠A＝100°，点E、F在BC上，OE平分∠BOF，且∠FOC＝∠AOC，下列结论中正确的是___________：
①OB∥AC ②∠EOC＝45°
③∠OCB：∠OFB＝1：3 ④若∠OEB＝∠OCA，则∠OCA＝60°
查看答案和解析>>
科目：初中数学 来源： 题型：
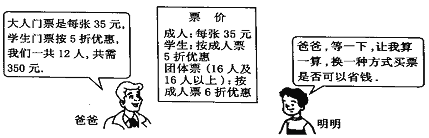
【题目】春节期间，七年级(1)班的明明、丽丽等同学随家长一同到某公园游玩，如图是购买门票时，明明与他爸爸的对话，试根据图中的信息，解答下列问题：
(1)明明他们一共去了几个成人?几个学生？
(2)请你帮助明明算一算，用哪种方式购票更省钱?
(3)购完票后，明明发现七年级(2)班的张小涛等8个学生和他们的12个家长共20人也来购票，请你为他们设计出最省钱的购票方案，并求出此时的购票费用。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
