
【题目】已知,BC∥OA,∠B=∠A=100°,点E、F在BC上,OE平分∠BOF,且∠FOC=∠AOC,下列结论中正确的是___________:

①OB∥AC ②∠EOC=45°
③∠OCB:∠OFB=1:3 ④若∠OEB=∠OCA,则∠OCA=60°
【答案】①④
【解析】试题解析:①∵BC∥OA,
∴![]() ,又∵∠B=∠A,
,又∵∠B=∠A,
∴∠A+∠O=![]() ,
,
∴OB∥AC;故①正确.
②∵![]()
∴![]()
∵OE平分∠BOF,
∴∠BOE=∠EOF,又∵∠FOC=∠AOC,
![]() 故②错误.
故②错误.
③结论:∠OCB:∠OFB的值不发生变化,理由为:
∵BC∥OA,
∴∠FCO=∠COA,
又∵∠FOC=∠AOC,
∴∠FOC=∠FCO,
∴∠OFB=∠FOC+∠FCO=2∠OCB,
∴∠OCB:∠OFB=1:2;
故③错误.
④由①知:OB∥AC,
则∠OCA=∠BOC,
由②可以设:∠BOE=∠EOF=α,∠FOC=∠COA=β,
则∠OCA=∠BOC=2α+β,
∠OEB=∠EOC+∠ECO=α+β+β=α+2β,
∵∠OEB=∠OCA,
∴2α+β=α+2β,
∴α=β,
∵![]()
∴![]()
![]()
故④正确.
故答案为:①④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,某小区内有一块长、宽比为2∶1的矩形空地,计划在该空地上修筑两条宽均为2 m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312 m2,请求出原来大矩形空地的长和宽.
(1)请找出上述问题中的等量关系:_________________;
(2)若设大矩形空地的宽为xm,可列出的方程为_____________,方程的解为__________,原来大矩形空地的长和宽分别为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
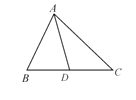
【题目】如图所示,AD是△ABC的边BC的中线.
(1)画出以点D为对称中心,与△ABD成中心对称的三角形;
(2)若AB=10,AC=12,求AD长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件能保证△ABC≌△ADC的是:①AB=AD,BC=DC;②∠1=∠3,∠4=∠2;③∠1=∠2,∠4=∠3;④∠1=∠2,AB=AD;⑤∠1=∠2,BC=DC.( )
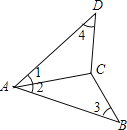
A. ①②③④⑤ B. ①②③④ C. ①③④ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
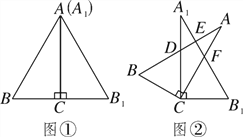
【题目】将两块相同的含30°角的直角三角板按图①的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图②的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
(1)当旋转角等于20°时,∠BCB1=________度;
(2)当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:
定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加、减,乘法运算与整式的加、减、乘法运算类似.
例如计算:(2-i)+(5+3i)=(2+5)+(-1+3)i=7+2i;
(1+i)×(2-i)=1×2-i+2×i-i2=2+(-1+2)i+1=3+i;
根据以上信息,完成下列问题:
(1)填空:i3= ,i4= ;
(2)计算:(1+i)×(3-4i);
(3)计算:i+i2+i3+…+i2018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 问题发现:如图
问题发现:如图![]() ,直线
,直线![]() 是AB与AD之间的一点,连接
是AB与AD之间的一点,连接![]() ,可以发现
,可以发现![]() .
.
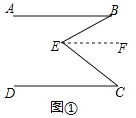

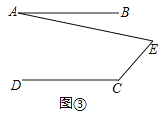
请把下面的证明过程补充完整:
证明:过点E作![]() ,
,
![]() 已知
已知![]() 辅助线的作法
辅助线的作法![]() .
.
![]() _____
_____![]()
![]() ______
______
![]() 同理
同理![]() .
.
![]() _____
_____![]()
等量代换![]()
即![]() .
.
![]() 拓展探究:如果点E运动到图
拓展探究:如果点E运动到图![]() 所示的位置,其他条件不变,进一步探究发现:
所示的位置,其他条件不变,进一步探究发现: ![]() ,请说明理由.
,请说明理由.
![]() 解决问题:如图
解决问题:如图![]() ,请直接写出
,请直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=![]() ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )

A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com