
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬Οφ≤ΡΝœΘΚ
Ε‘”ΎΤΫΟφΆΦ–ΈAΘ§»γΙϊ¥φ‘Ύ“ΜΗω‘≤Θ§ ΙΆΦ–ΈA…œΒΡ»Έ“β“ΜΒψΒΫ‘≤–ΡΒΡΨύάκΕΦ≤Μ¥σ”Ύ’βΗω‘≤ΒΡΑκΨΕΘ§‘ρ≥ΤΆΦ–ΈA±Μ’βΗω‘≤ΥυΗ≤Η«.
Ε‘”ΎΤΫΟφΆΦ–ΈAΘ§»γΙϊ¥φ‘ΎΝΫΗωΜρΝΫΗω“‘…œΒΡ‘≤Θ§ ΙΆΦ–ΈA…œΒΡ»Έ“β“ΜΒψΒΫΤδ÷–Ρ≥Ηω‘≤ΒΡ‘≤–ΡΒΡΨύάκΕΦ≤Μ¥σ”Ύ’βΗω‘≤ΒΡΑκΨΕΘ§‘ρ≥ΤΆΦ–ΈA±Μ’β–©‘≤ΥυΗ≤Η«.
άΐ»γΘΚΆΦ1÷–ΔΌΒΡ»ΐΫ«–Έ±Μ“ΜΗω‘≤Η≤Η«Θ§ΔΎ÷–ΒΡΥΡ±Ώ–Έ±ΜΝΫΗω‘≤ΥυΗ≤Η«.

ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
(1)±Ώ≥ΛΈΣ1 cmΒΡ’ΐΖΫ–Έ±Μ“ΜΗωΑκΨΕΈΣrΒΡ‘≤ΥυΗ≤Η«Θ§rΒΡΉν–Γ÷Β «______ cm;
(2)±Ώ≥ΛΈΣ1 cmΒΡΒ»±Ώ»ΐΫ«–Έ±Μ“ΜΗωΑκΨΕΈΣrΒΡ‘≤ΥυΗ≤Η«Θ§rΒΡΉν–Γ÷Β «_____ cm;
(3)≥ΛΈΣ2 cmΘ§ΩμΈΣ1 cmΒΡΨΊ–Έ±ΜΝΫΗωΑκΨΕΨυΈΣrΒΡ‘≤ΥυΗ≤Η«Θ§rΒΡΉν–Γ÷Β «_____ cm.’βΝΫΗω‘≤ΒΡ‘≤–ΡΨύ «_____ cm.ΓΘ
ΓΨ¥πΑΗΓΩΘ®1) ![]() ΘΜ
ΘΜ
(2)![]() ΘΜ
ΘΜ
(3) ![]() Θ§ 1.
Θ§ 1.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©±Ώ≥ΛΈΣ1 cmΒΡ’ΐΖΫ–Έ±Μ“ΜΗωΑκΨΕΈΣrΒΡ‘≤ΥυΗ≤Η«Θ§‘ρr”Π¥σ”ΎΒ»”Ύ’ΐΖΫ–ΈΕ‘Ϋ«œΏΒΡ“ΜΑκΘ§Φ¥ΑκΨΕΉν–ΓΈΣ![]() ΘΜΘ®2Θ©Β±‘≤ΆβΫ”»ΐΫ«–Έ ±‘≤ΒΡΑκΨΕΉν–ΓΘ§»γΆΦΘ§ΗυΨίΙ¥Ι…Ε®άμΩ…«σΒΟ‘≤ΒΡΑκΨΕ «
ΘΜΘ®2Θ©Β±‘≤ΆβΫ”»ΐΫ«–Έ ±‘≤ΒΡΑκΨΕΉν–ΓΘ§»γΆΦΘ§ΗυΨίΙ¥Ι…Ε®άμΩ…«σΒΟ‘≤ΒΡΑκΨΕ «![]() ΘΜΘ®3Θ©ΗυΨίΕ‘≥Τ–‘Ω…÷ΣΝΫ‘≤ΒΡΫΜΒψΖ÷±π «ADΚΆBCΒΡ÷–ΒψΘ§ΫΪΨΊ–ΈΖ÷≥…ΝΫΗωœύΒ»ΒΡ–Γ’ΐΖΫ–ΈΘ§‘≤ΒΡΉν–ΓΑκΨΕΨΆ «–Γ’ΐΖΫ–ΈΒΡΕ‘Ϋ«œΏΒΡ“ΜΑκΘ§‘≤–ΡΨύΨΆ «–Γ’ΐΖΫ–ΈΒΡ±Ώ≥Λ.
ΘΜΘ®3Θ©ΗυΨίΕ‘≥Τ–‘Ω…÷ΣΝΫ‘≤ΒΡΫΜΒψΖ÷±π «ADΚΆBCΒΡ÷–ΒψΘ§ΫΪΨΊ–ΈΖ÷≥…ΝΫΗωœύΒ»ΒΡ–Γ’ΐΖΫ–ΈΘ§‘≤ΒΡΉν–ΓΑκΨΕΨΆ «–Γ’ΐΖΫ–ΈΒΡΕ‘Ϋ«œΏΒΡ“ΜΑκΘ§‘≤–ΡΨύΨΆ «–Γ’ΐΖΫ–ΈΒΡ±Ώ≥Λ.
Θ®1)“‘’ΐΖΫ–ΈΒΡΕ‘Ϋ«œΏΈΣ÷±ΨΕΉω‘≤ «Η≤Η«’ΐΖΫ–ΈΒΡΉν–Γ‘≤Θ§ΑκΨΕrΒΡΉν–Γ÷ΒΘΫ![]() ;
;
(2) ±Ώ≥ΛΈΣ1 cmΒΡΒ»±Ώ»ΐΫ«–Έ±Μ“ΜΗωΑκΨΕΈΣrΒΡ‘≤ΥυΗ≤Η«Θ§’βΗωΉν–ΓΒΡ‘≤ «’ΐ»ΐΫ«–ΈΒΡΆβΫ”‘≤Θ§»γΆΦΉς»ΐΫ«–ΈABCΒΡΗΏADΙΙ≥…÷±Ϋ«»ΐΫ«–ΈABDΘ§–±±ΏABΘΫ1Θ§BDΘΫ![]() Θ§
Θ§
Υυ“‘ADΘΫΘ§“ρΈΣ»ΐΫ«–Έ «’ΐ»ΐΫ«–ΈΘ§
Υυ“‘ΓœABCΘΫ60ΓψΘ§O «Άβ–ΡΘ§Υυ“‘ΓœOBC=30ΓψΘ§ODΘΫ![]() OBΘ§
OBȧ
…ηOAΘΫOB=xΘ§‘ρODΘΫ![]() xΘ§
xȧ
‘Ύ÷±Ϋ«»ΐΫ«–ΈOBD÷–Θ§ΗυΨίΙ¥Ι…Ε®άμΝ–ΖΫ≥ΧΘΚΘ§
 ΫβΒΟΘΚxΘΫ
ΫβΒΟΘΚxΘΫ![]() .
.
(3)»γΆΦΘΚΨΊ–ΈABCD÷–ABΘΫ1Θ§BCΘΫ2Θ§
‘ρΗ≤Η«ABCDΒΡΝΫΗω‘≤”κΨΊ–ΈΫΜ”ΎEΓΔFΝΫΒψΘ§
”…Ε‘≥Τ–‘÷ΣEΓΔFΖ÷±π «ADΚΆBCΒΡ÷–ΒψΘ§
‘ρΥΡ±Ώ–ΈABFEΓΔEFCD «ΝΫΗω±Ώ≥ΛΈΣ1ΒΡ’ΐΖΫ–ΈΘ§
Υυ“‘‘≤ΒΡΑκΨΕrΘΫ![]() , ΝΫ‘≤–ΡΨύΘΫ 1.
, ΝΫ‘≤–ΡΨύΘΫ 1.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓςABC»ΐΗωΕΞΒψΒΡΉχ±ξΖ÷±πΈΣΘ®1Θ§2Θ©Θ§Θ®-2Θ§3Θ©Θ§Θ®-1Θ§0Θ©Θ§Α―ΥϋΟ«ΒΡΚαΉχ±ξΚΆΉίΉχ±ξΕΦά©¥σΒΫ‘≠ά¥ΒΡ2±ΕΘ§ΒΟΒΫΒψ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ°œ¬Ν–ΥΒΖ®’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
Θ°œ¬Ν–ΥΒΖ®’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©

A. Γς![]() ”κΓςABC «ΈΜΥΤΆΦ–ΈΘ§ΈΜΥΤ÷––Ρ «ΒψΘ®1Θ§0Θ©
”κΓςABC «ΈΜΥΤΆΦ–ΈΘ§ΈΜΥΤ÷––Ρ «ΒψΘ®1Θ§0Θ©
B. Γς![]() ”κΓςABC «ΈΜΥΤΆΦ–ΈΘ§ΈΜΥΤ÷––Ρ «ΒψΘ®0Θ§0Θ©
”κΓςABC «ΈΜΥΤΆΦ–ΈΘ§ΈΜΥΤ÷––Ρ «ΒψΘ®0Θ§0Θ©
C. Γς![]() ”κΓςABC «œύΥΤΆΦ–ΈΘ§ΒΪ≤Μ «ΈΜΥΤΆΦ–Έ
”κΓςABC «œύΥΤΆΦ–ΈΘ§ΒΪ≤Μ «ΈΜΥΤΆΦ–Έ
D. Γς![]() ”κΓςABC≤Μ «œύΥΤΆΦ–Έ
”κΓςABC≤Μ «œύΥΤΆΦ–Έ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥ¥”ΦΉΓΔ““ΝΫΟϊ―Γ ÷÷–―ΓΑΈ“Μ»Υ≤ΈΦ”…δΜς±»»ϋΘ§œ÷Ε‘ΥϊΟ«Ϋχ––“Μ¥Έ≤β―ιΘ§ΝΫΗω»Υ‘ΎœύΆ§ΧθΦΰœ¬Ης…δΑ–10¥ΈΘ§ΈΣΝΥ±»ΫœΝΫ»ΥΒΡ≥…Φ®Θ§÷ΤΉςΝΥ»γœ¬Ά≥ΦΤΆΦ±μΘΚ

ΦΉΓΔ““…δΜς≥…Φ®Ά≥ΦΤ±μ
ΤΫΨυ ΐ | ÷–ΈΜ ΐ | ΖΫ≤ν | Οϋ÷–10ΜΖΒΡ¥Έ ΐ | |
ΦΉ | 7 | |||
““ | 1 |
(1)«κ≤Ι»Ϊ…œ ωΆΦ±μ(«κ÷±Ϋ”‘Ύ±μ÷–ΧνΩ’ΚΆ≤Ι»Ϊ’έœΏΆΦ)ΘΜ
(2)»γΙϊΙφΕ®≥…Φ®ΫœΈ»Ε®’Ώ Λ≥ωΘ§Ρψ»œΈΣΥ≠ΫΪ Λ≥ωΘΩΥΒΟςΡψΒΡάμ”…ΘΜ
(3)»γΙϊœΘΆϊ(2)÷–ΒΡΝμ“ΜΟϊ―Γ ÷ Λ≥ωΘ§ΗυΨίΆΦ±μ÷–ΒΡ–≈œΔΘ§”ΠΗΟ÷ΤΕ®‘θ―υΒΡΤά≈–Ιφ‘ρΘΩΈΣ ≤Ο¥ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΡΕΝΫβΧβΙΐ≥Χ,ΜΊ¥πΈ Χβ.
»γΆΦ,OC‘ΎΓœAOBΡΎ,ΓœAOBΚΆΓœCODΕΦ «÷±Ϋ«,«“ΓœBOC=30Γψ,«σΓœAODΒΡΕ» ΐ.
Ϋβ:ΙΐOΒψΉς…δœΏOM, ΙΒψM,O,A‘ΎΆ§“Μ÷±œΏ…œ.
“ρΈΣΓœMOD+ΓœBOD=90Γψ,ΓœBOC+ΓœBOD=90Γψ,Υυ“‘ΓœBOC=ΓœMOD,
Υυ“‘ΓœAOD=180Γψ-ΓœBOC=180Γψ-30Γψ=150Γψ.
(1)»γΙϊΓœBOC=60Γψ,Ρ«Ο¥ΓœAODΒ»”ΎΕύ…ΌΕ»?»γΙϊΓœBOC=nΓψ,Ρ«Ο¥ΓœAODΒ»”ΎΕύ…ΌΕ»?
(2)»γΙϊΓœAOB=ΓœDOC=xΓψ,ΓœAOD=yΓψ,«σΓœBOCΒΡΕ» ΐ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ“Μ’≈»ΐΫ«–Έ÷ΫΤ§ABCΘ®»γΆΦΦΉΘ©Θ§Τδ÷–AB=ACΘ°ΫΪ÷ΫΤ§―ΊΙΐΒψBΒΡ÷±œΏ’έΒΰΘ§ ΙΒψC¬δΒΫAB±Ώ…œΒΡEΒψ¥ΠΘ§’έΚέΈΣBDΘ®»γΆΦ““Θ©Θ°‘ΌΫΪ÷ΫΤ§―ΊΙΐΒψEΒΡ÷±œΏ’έΒΰΘ§ΒψA«ΓΚΟ”κΒψD÷ΊΚœΘ§’έΚέΈΣEFΘ®»γΆΦ±ϊΘ©Θ°‘≠»ΐΫ«–Έ÷ΫΤ§ABC÷–Θ§ΓœABCΒΡ¥σ–ΓΈΣ______ΓψΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚΓςABC‘ΎΉχ±ξΤΫΟφΡΎΘ§»ΐΗωΕΞΒψΒΡΉχ±ξΖ÷±πΈΣAΘ®0Θ§3Θ©Θ§BΘ®3Θ§4Θ©Θ§CΘ®2Θ§2Θ©.Θ®’ΐΖΫ–ΈΆχΗώ÷–Θ§ ΟΩΗω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥Λ «1ΗωΒΞΈΜ≥ΛΕ»Θ©
Θ®1Θ©Μ≠≥ωΓςABCœρœ¬ΤΫ“Τ4ΗωΒΞΈΜΒΟΒΫΒΡΓςA1B1C1Θ§≤Δ÷±Ϋ”–¥≥ωC1ΒψΒΡΉχ±ξΘΜ
Θ®2Θ©“‘ΒψBΈΣΈΜΥΤ÷––ΡΘ§‘ΎΆχΗώ÷–Μ≠≥ωΓςA2BC2Θ§ ΙΓςA2BC2”κΓςABCΈΜΥΤΘ§«“ΈΜΥΤ±»ΈΣ2©U1Θ§≤Δ÷±Ϋ”–¥≥ωC2ΒψΒΡΉχ±ξΦΑΓςA2BC2ΒΡΟφΜΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ÷±œΏl1ΓΈl2Θ§÷±œΏl3ΚΆ÷±œΏl1ΓΔl2ΫΜ”ΎΒψCΚΆDΘ§ΒψP «÷±œΏl3…œ“ΜΕ·Βψ
Θ®1Θ©»γΆΦ1Θ§Β±ΒψP‘ΎœΏΕΈCD…œ‘ΥΕ· ±Θ§ΓœPACΘ§ΓœAPBΘ§ΓœPBD÷°Φδ¥φ‘Ύ ≤Ο¥ ΐΝΩΙΊœΒΘΩ«κΡψ≤¬œκΫα¬έ≤ΔΥΒΟςάμ”…Θ°
Θ®2Θ©Β±ΒψP‘ΎCΓΔDΝΫΒψΒΡΆβ≤ύ‘ΥΕ· ±Θ®PΒψ![]() ”κΒψCΓΔD≤Μ÷ΊΚœΘ§»γΆΦ2ΚΆΆΦ3Θ©Θ§…œ ωΘ®1Θ©÷–ΒΡΫα¬έ «ΖώΜΙ≥…ΝΔΘΩ»τ≤Μ≥…ΝΔΘ§«κ÷±Ϋ”–¥≥ωΓœPACΘ§ΓœAPBΘ§ΓœPBD÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤Μ±Ί–¥άμ”…Θ°
”κΒψCΓΔD≤Μ÷ΊΚœΘ§»γΆΦ2ΚΆΆΦ3Θ©Θ§…œ ωΘ®1Θ©÷–ΒΡΫα¬έ «ΖώΜΙ≥…ΝΔΘΩ»τ≤Μ≥…ΝΔΘ§«κ÷±Ϋ”–¥≥ωΓœPACΘ§ΓœAPBΘ§ΓœPBD÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤Μ±Ί–¥άμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ

ΔΌ ΓΏ![]()
Γύ ______// _____Θ®______________________Θ©
ΔΎΓΓΓΏΓœDAB+ΓœABC=180Γψ
Γύ _____// _____Θ®__________________Θ©
ΔέΓΏ AB // CD
ΓύΓœ_____+ΓœABC=180ΓψΘ®___________________Θ©
ΔήΓΏ ______// ______
ΓύΓœC=Γœ3Θ®_______________________Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΑκΨΕΨυΈΣ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΑκ‘≤O1ΓΔO2ΓΔO3Θ§Γ≠Ήι≥…“ΜΧθΤΫΜ§ΒΡ«ζœΏΘ§ΒψP¥”‘≠ΒψO≥ωΖΔΘ§―Ί’βΧθ«ζœΏœρ”“‘ΥΕ·Θ§ΥΌΕ»ΈΣΟΩΟκ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§‘ρΒΎ2015Οκ ±Θ§ΒψPΒΡΉχ±ξ «Θ® Θ©
ΗωΒΞΈΜ≥ΛΕ»Θ§‘ρΒΎ2015Οκ ±Θ§ΒψPΒΡΉχ±ξ «Θ® Θ©
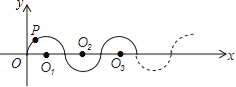
A. Θ®2014Θ§0Θ© B. Θ®2015Θ§©¹1Θ© C. Θ®2015Θ§1Θ© D. Θ®2016Θ§0Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com