
����Ŀ�����˽���̫���������ٺ�����̫���˲���֮����������ٺ����кס��������зֱ���12000Ԫ����ͬ�Ľ��۹���������ͬ�İٺϣ��׳������۷����ǣ����ٺϰ������װ���ۣ������������ʵİٺ�400ǧ�ˣ��Խ��۵�2���۸����ۣ�ʣ�µİٺ��Ը��ڽ���10%���ۣ��ҳ��е����۷����ǣ������ٺϷ��ֱ࣬�Ӱ�װ���ۣ��۸׳��з������۵����ְٺϵ��ۺ͵�һ�붨�ۣ��������н��ٺ�ȫ�����꣬���м׳��л���8400Ԫ�������ɱ����ƣ����ʣ�
��1���ٺϽ���Ϊÿǧ�˶���Ԫ��
��2���ҳ��л�������Ԫ�����Ƚ��������۷�ʽ�����㣮
���𰸡�(1)��20Ԫ��(2)��6600Ԫ���׳������۷�ʽ������.
��������
���������(1)��������ٺϽ���Ϊÿǧ��xԪ��Ȼ����������г���ʽ���̣��Ӷ����x��ֵ�������Ҫ����������ó��𰸣�(2)�����������������Ȼ��ó��ҳ��е��ۼۣ��Ӷ��ó��ҳ��еĻ�����Ȼ����бȽϴ�С�ó���.
���������(1)����ٺϽ���Ϊÿǧ��xԪ��
��������ã�![]()
��ã�x=20��
������x=20�Ƿ�ʽ���̵Ľ⣬�ҷ������⣬�ٺϽ���Ϊÿǧ��20Ԫ��
(2)��������Ϊ![]() =600��ǧ�ˣ����ҳ����ۼ�Ϊ����20��2+1.1��20����2=31��Ԫ/ǧ�ˣ���
=600��ǧ�ˣ����ҳ����ۼ�Ϊ����20��2+1.1��20����2=31��Ԫ/ǧ�ˣ���
�ҳ��л���Ϊ600����31��20��=6600��Ԫ����6600��8400����׳������۷�ʽ�����࣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����P������������һ�㣬����APB=��ABC��

��1����ͼ1������BAC=60������Pǡ������ABC��ƽ�����ϣ�PA=2����PB�ij���
��2����ͼ2������BAC=60����̽��PA��PB��PC��������ϵ����֤����
��3����ͼ3������BAC=120������ֱ��д��PA��PB��PC��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ����֪����y= (x��0)ͼ����һ��P��PA��x���ڵ�A��a��0������B����Ϊ��0��b��(b>0) ������M��y���������ϵ�B�Ϸ��ĵ㣮����N������AP�ϣ�����B��AB�Ĵ��ߣ�������AP�ڵ�D����ֱ��MN�ڵ�Q������AQ��ȡAQ���е�C��
(1)��ͼ2������BP������PAB�������
(2)����Q���߶�BD��ʱ, ���ı���BQNC�����Σ����Ϊ2�����ʱP������꣮
(3)��(2)�������£���ƽ��ֱ������ϵ���Ƿ���ڵ�S��ʹ���Ե�D��Q��N��SΪ������ı���Ϊƽ���ı�
�Σ�������ڣ���ֱ��д�����еĵ�S�����ꣻ��������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ������ ��
A. a2��a3��a6 B. ����2ab��2��4a2b2 C. ��a2��3��a5 D. a6��a3��a2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±�����Ϊij�̵걡�������������ij��Ʒԭ��Ϊ560Ԫ�����Ų�ͬ���ȵĽ��ۣ�����������λΪ����������Ӧ�ı仯������ۼ�Ϊ500Ԫʱ��������Ϊ�� ������
���ۣ�Ԫ�� | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
������������ | 780 | 810 | 840 | 870 | 900 | 930 | 960 |
A.1200
B.750
C.1110
D.1140
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ������ε��ڽǺ͵���������Ǻͣ����������εı���Ϊ
A. 3 B. 4 C. 5 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
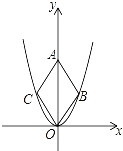
����Ŀ�����κ���y=![]() x2��ͼ����ͼ����OΪ����ԭ�㣬��A��y����������ϣ���B��C�ڶ��κ���y=
x2��ͼ����ͼ����OΪ����ԭ�㣬��A��y����������ϣ���B��C�ڶ��κ���y=![]() x2��ͼ���ϣ��ı���OBACΪ���Σ�����OBA=120����������OBAC�����Ϊ ��
x2��ͼ���ϣ��ı���OBACΪ���Σ�����OBA=120����������OBAC�����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е����У��ʺ��ղ���ǣ� ����
A. ��ѧ����ϲ���ĵ��ӽ�Ŀ
B. ij���Ծ��ϵ�ӡˢ����
C. �ʼ첿�ŶԸ����������ĵ��ʹ�������ĵ���
D. ��ѧ���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com