练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

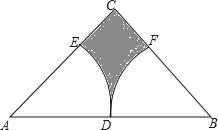
    【题目】如图，在等腰直角三角形ABC中，∠C=90°，点D为AB的中点，已知扇形EAD和扇形FBD的圆心分别为点A、点B，且AB=4，则图中阴影部分的面积为_____（结果保留π）．

    【答案】4﹣π

    【解析】

    由在等腰直角三角形ABC中，∠C=90°，AB=4，可求得直角边AC与BC的长，继而求得△ABC的面积，又由扇形的面积公式求得扇形EAD和扇形FBD的面积，继而求得答案．

    解：∵在等腰直角三角形ABC中，∠C=90°，AB=4，

    ∴AC=BC=ABsin45°=AB=2，

    ∴S△ABC=ACBC=4，

    ∵点D为AB的中点，

    ∴AD=BD=AB=2，

    ∴S扇形EAD=S扇形FBD=×π×22=π，

    ∴S阴影=S△ABC﹣S扇形EAD﹣S扇形FBD=4﹣π．

    故答案为：4﹣π．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】大家看过中央电视台“购物街”节目吗？其中有一个游戏环节是大转轮比赛，转轮上平均分布着5、10、15、20一直到100共20个数字．选手依次转动转轮，每个人最多有两次机会．选手转动的数字之和最大不超过100者为胜出；若超过100则成绩无效，称为“爆掉”．

    (1)某选手第一次转到了数字5，再转第二次，则他两次数字之和为100的可能性有多大？

    (2)现在某选手第一次转到了数字65，若再转第二次了则有可能“爆掉”，请你分析“爆掉”的可能性有多大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在梯形ABCD中，∠A=∠B=90°，AB=，点E在AB上，∠AED=45°，DE=6，CE=7.

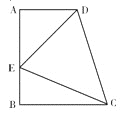
    （1）求AE的长；

    （2）求sin∠BCE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠C＝90°，点D为AC上一点，∠ABD＝2∠BAC＝45°，若AD＝12，则△ABD的面积为____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为丰富学生课外活动，某校积极开展社团活动，开设的体育社团有：A：篮球，B：排球，C：足球，D：羽毛球，E：乒乓球．学生可根据自己的爱好选择一项，李老师对八年级同学选择体育社团情况进行调查统计，制成了两幅不完整的统计图（如图），则以下结论不正确的是（　　）

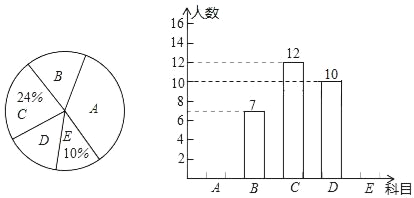
    A. 选科目E的有5人

    B. 选科目A的扇形圆心角是120°

    C. 选科目D的人数占体育社团人数的

    D. 据此估计全校1000名八年级同学，选择科目B的有140人

    查看答案和解析>>

    科目：初中数学 来源： 题型：

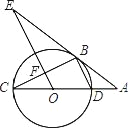
    【题目】如图，CD为⊙O的直径，点B在⊙O上，连接BC、BD，过点B的切线AE与CD的延长线交于点A，OE∥BD，交BC于点F，交AE于点E．

    （1）求证：△BEF∽△DBC．

    （2）若⊙O的半径为3，∠C=30°，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

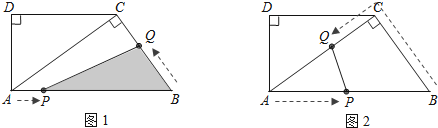
    【题目】如图1，DC∥AB，∠D=90°，AC⊥BC，AB=10cm，BC=6cm. 点P以1cm/s的速度从点A出发，沿AB方向向点B运动，同时点Q以2cm/s的速度从点B出发，沿B→C→A方向向点A运动，当一个运动点到达终点时，另一个运动点也随之停止运动，设运动的时间为t(s).

    （1）① 求证：△ACD∽△BAC；② 求DC的长；

    （2）当点Q在边BC上运动，求t为何值时，△PBQ的面积为cm2；

    （3）如图2，当点Q在边CA上运动，求t为何值时，PQ∥BC.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知．按照以下步骤作图：①以点为圆心，以适当的长为半径作弧，分别交的两边于两点，连接．②分别以点为圆心，以大于线段的长为半径作弧，两弧在内交于点，连接．③连接交于点．下列结论中错误的是( )

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知一次函数y=kx+4图象交直线OA于点A(1,2)，交y轴于点B，点C为坐标平面内一点.

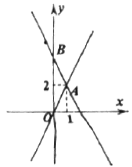
    (1)求k值;

    (2)若以O、A、B、C为顶点的四边形为菱形，则C点坐标为 ；

    (3)在直线AB上找点D，使△OAD的面积与((2)中菱形面积相等，则D点坐标为 .

    查看答案和解析>>

    同步练习册答案